ONLINE CLASS 6: 6 MATHEMATICS 2021-2022

R/43
02/03/2022 - 12/03/2022

R/42
22/02/2022 - 26/02/2022

REVISION OF CHAPTER-15 AND CHAPTER-04

CHAPTER-04

ASSIGNMENT

Revise Chapter-15 full and Chapter-04, Ex's A and B, do Mental Maths, MCQs and Chapter Test, pages 86-87 in Maths practical book.

R/41
21/02/2022

CLASS TEST OF CHAPTER-14.

ASSIGNMENT

REVISE CH-15, EX-A.

R/40
15/02/2022, 16/02/2022, 17/02/2022, 18/02/2022, 19/02/2022

REVISION OF CHAPTER-14 PERIMETER AND AREA

ASSIGNMENT

Revise Ch-14 all exercises, Mental Maths, MCQs and Chapter Test for class test on 21/02/2022.

R/39
11/02/2022, 12/02/2022, 14/02/2022

Ch-13 Basic Constructions ( Using ruler and compasses )

(Download Ch-13 in pdf by clicking on the chapter's name above.)

TOPIC

Construct perpendicular line segments

Construct angles of different measures using compasses

EXPLAINED

Construct perpendicular line segments

Construct angles of different measures using compasses

MUST WATCH FOR BETTER UNDERSTANDING

Video-01 Practical Geometry

Video-02 Geometrical Constructions

Main Teachings

Oral Explanation Online with some written work.

Practical geometry is an important branch of geometry which deals with the study of the size, positions, shapes as well as dimensions of objects.

Geometrical Instruments

Whether you have to draw a line segment or measure it, draw a circle or arcs, draw an angle, etc. it can easily be possible with the help of geometrical tools. Let us discuss the various geometrical instruments used in practical geometry.

Name of Geometrical tool	Use of Geometrical tool
Divider	Comparing lengths.
Protractor	Measure as well as draw angles.
Set Squares	To draw parallel and perpendicular lines.
Compass	To draw circles, arcs, and to mark equal lengths.
Ruler	To measure lengths of the line segment and to draw a line segment.

Point: It is a location.

Line: Collection of points in a linear manner that extends infinitely in two directions.

Tools of Construction

Tools used for construction:
Ruler: An instrument used to draw line segments and measure their lengths.
Compass: Instrument having a pointer on one end and a pencil on the other end. It is used to mark equal lengths and to draw circles and arcs.
Divider: Instrument having a pair of pointers. It is used to compare lengths.
Set- Squares: Two triangular pieces – One of them has 45°, 45°, 90° and the other has 30°, 60°, 90° angles at the vertices. It is used to draw parallel and perpendicular lines.
Protractor: A semicircular instrument graduated into 180° parts. It is used to draw and measure angles.

Line Segment

Line Segment: Part of a line that is bounded by two distinct endpoints.
Constructing a Line Segment for a given Length
Steps for constructing a line segment of a given length ‘a’:
(i) Draw a line l and mark a point A on it.
(ii) Place the compass on the initial point of the ruler. Open it to place pencil point up to the ‘a’ mark.
(iii) Place the pointer on A and draw an arc to cut l at B. AB is the required line segment.
Constructing Copy of a Line Segment
Steps for constructing a copy of a given line segment using ruler and compass together:
(i) Given AB whose length is unknown.
(ii) Fix compass’ pointer on A and pencil end on B. The opening of the instrument now gives the length of AB.
(iii) Draw any line l.
(iv) Placing the pointer on C, draw an arc that cuts l at a point say D. Then, CD = AB.

Perpendiculars and Parallels
A line MN meeting another line AB at the right angle is said to be the perpendicular to the line AB.
If two lines are non-intersecting and are always the same distance apart, then they are said to be parallel lines.
As shown in the figure, AB || CD.
Constructing a Perpendiculars Using a Compass and Ruler
Steps for constructing perpendiculars using compass and rulers:
(i) Given a line I and a point P not on it.
(ii) With P as the centre, draw an arc which intersects line I at two points A and B.
(iii) Using the same radius and with A and B as centres, construct two arcs that intersect at a point, say Q, on the other side.
(iv) Join PQ. Thus, $\bar{P Q}$ is the perpendicular to l.
Constructing Perpendicular to a Line through a Point on the Line
Steps to construct a perpendicular to a line through a point on the line:
(i) Place a ruler along a given line l such that one of its edges is along l.
(ii) Place a set square with one of its edges along the already aligned edge of the ruler.
(iii) Slide the set square such that its right-angled corner coincides with the Point P.
(iv) Draw PQ and PQ are perpendicular to l.
Paper Folding Construction
Paper folding method to make perpendiculars:
(i) Let l be the given line and P be a point outside l.
(ii) Place a set-square on l such that one arm of its right angle aligns along l.
(iii) Place a ruler along the edge opposite to the right angle of the set-square.
(iv) Slide the set-square along the ruler till the point P touches the other arm of the set-square.
Circle
A circle is a set of all points in a plane that are equidistant from a point i.e. centre of the circle.
Construction of a Circle for a given Radius
Steps for constructing a circle using a compass:
(i) Open compass for the required radius.
(ii) Place pointer of the compass on O.
(iii) Rotate the compass slowly to draw the circle.
How to Construct an Angle
Angle Bisector and Its Construction
Steps to construct angle bisectors of a given angle:
(i) With O as the centre, draw an arc that cuts both rays at A and B.
(ii) With B as the centre, draw an arc whose radius is more than half of the length of AB.
(iii) With A as the centre, with the same radius, cut an arc in the interior of ∠BOA
(iv) Mark point of intersection as C. Then, OC is the angle bisector.
Construction of 30°, 60°, 90°and 120°Angles
(i) Construction of 60° angle:
(ii) Construction of 120°angle:
(iii) Construction of 90° angle:
(iv) Construction of 30° angle:
Constructing of an Angle with Unknown Measurement
Steps for constructing a copy of an angle with unknown measurement:
(i) Draw a line l and choose a point P on it.
(ii) Place compass’ pointer at A and draw an arc to cut the rays of ∠A at B and C.
(iii) Draw an arc with P as the centre, cutting /at Q.
(iv) Set your compasses to length BC with the same radius.
(v) Place the compasses pointer at Q and draw an arc to cut the arc drawn earlier in R.
(vi) Join PR. This gives ∠P=∠A
Angles
Angles: Formed by two rays sharing a common endpoint.
ASSIGNMENT
Study and practice Ch-13 and do Self Practice 13 full, page-230.

R/38
10/02/2022
PERIODIC TEST-04

ASSIGNMENT

Revise Ch-06, Ex's A and B.

R/37
09/02/2022

REVISION OF CHAPTERS 12 AND 15

ASSIGNMENT

Revise for P.T-04 on 10/02/2022.

R/36
08/02/2022

CHAPTER-05 FRACTIONS ( REVISION )

ASSIGNMENT

Revise Chapter-5 Ex's A and B.

R/35
07/02/2022

CHAPTER-11 THREE DIMENSIONAL SHAPES

ASSIGNMENT

Do Chapter-11, Mental Maths, MCQs and Chapter Test in Maths practical book.

R/34

01/02/2022, 03/02/2022, 04/02/2022

Ch-12 2D LINEAR SYMMETRY

( REFLECTION SYMMETRY )

(Download Ch-12 in pdf by clicking on the chapter's name above.)

TOPIC

Understand the concept of reflection by looking at mirror images.

Observe and identify symmetrical objects and the line of symmetry through folding and cutting out congruent halves that exactly cover each other.

Understand reflection symmetry.

EXPLAINED

Understand the concept of reflection by looking at mirror images.

Observe and identify symmetrical objects and the line of symmetry through folding and cutting out congruent halves that exactly cover each other.

Understand reflection symmetry.

MUST WATCH FOR BETTER UNDERSTANDING

Video-01 Introduction

Video-02 Symmetrical and Asymmetrical

Video-03 Symmetry in Nature

Video-04 Reflection and Symmetry

Video-05 Line Symmetry

Main Teachings

Oral Explanation Online with some written work.

Line of symmetry

When a figure is folded along a line such a way that the two parts exactly fit on top of each other, then the figure is said to have a line symmetry.

Line of symmetry is the line which divides figure into two identical parts and these are mirror image of each others.

Sometimes human face can also show line of symmetry. But this is not applicable in all cases.

Sometimes, line of symmetry is neither vertical nor horizontal. The following figure shows line of symmetry but its not vertical or horizontal.

The dotted lines below are not lines of symmetry though they may cut the figures in halves, they don't create two exactly same parts.

Alphabets words and numbers showing line of symmetry

Some alphabets posses vertical line of symmetry while some shows horizontal line of symmetry.

The following alphabets show both vertical as well as horizontal lines of symmetry.

The alphabet O has infinite number of lines of symmetry.

The following alphabets doesn’t show any type of symmetry.

F G J L N P Q R S Z

There are few words which also shows line of symmetry.

Some of the numbers also shows line of symmetry.

Geometric shapes which show one line of symmetry

Angle

An angle bisector is the only line of symmetry for a given angle.

Isosceles triangle

The line containing the bisector of the vertex angle of an isosceles triangle is only line of symmetry for such a triangle.

Trapezium

The perpendicular bisector of the parallel sides of an isosceles trapezium is the only line of symmetry.

Kite

The line containing the ends of a kite is the only line of symmetry for a kite. It bisects the angles at the ends of the kite.

Semicircle

A semicircle has only one line of symmetry.

There are few geometric shapes which doesn’t show any line of symmetry.

Geometric shapes which show two line of symmetry

Rectangle

Both perpendicular bisectors of the sides of a rectangle are lines of symmetry.

Ellipse

The major and minor axis of ellipse are lines of symmetry.

Rhombus

Both the bisectors of the angles of a rhombus are lines of symmetry.

More figures with two lines of symmetry

Geometric shapes which show multiple line of symmetry

Circle

The circle shows infinite line of symmetry.

Regular polygons

Regular (Equilateral) triangle has 3 lines of symmetry.

Regular quadrilateral (square) has 4 lines of symmetry.

Regular pentagon has 5 lines of symmetry

Regular hexagon has 6 lines of symmetry.

Regular octagon has 8 lines of symmetry.

From above we can conclude that the number lines of symmetry for a regular polygon is equal to the number of sides of the regular polygon.

Reflection and Symmetry

A reflection can be seen in mirror or water or any shine surface. Observe the following beautiful picture. We can see the reflection of the mountain, trees and clouds in water.

When we keep any object in front of the mirror we see the image of that object in the other side of the mirror. This image is known as reflection of that object and it is symmetrical in nature. Here the mirror line acts as a line of symmetry.

Any object and its reflection have same size, shape and but its orientation will be different from the object.

Case 1: Object is in contact with the mirror.

Case 2: Object is slightly away from the mirror.

Check whether following figures are reflections of each other?

In 1^st example, the image looks exactly same as object. i.e its shape and size. But the reflected image should have opposite orientation as compared to the object. So this is not a reflection.

In the 2^nd example, shape and size of the reflected image is exactly same as the object but its orientation is opposite as compared to the object. Hence this is a reflection.

Applications of symmetry

We can use the concept of symmetry to complete the pattern. See the following example. Here we have to observe the symmetrical pattern on the left and then we can complete the pattern on the right.

Kaleidoscope

It is a cylindrical shaped device with mirrors containing different colored objects like pebbles and pieces of glass. When we view from one end, light entering the other side creates a colourful pattern, due to the reflection of the mirrors. We can see the following types of patterns.

Rangoli design

Rangoli can be created with the help of symmetry.

While drawing rangoli, initially we draw some design and then we keep drawing the mirror image of earlier design. In this way the whole rangoli design is created.

ASSIGNMENTS

Do Chapter-12 all exercises, MCQs and Chapter test.

R/33

25/01/2022, 28/01/2022

ASSIGNMENTS

Revise Chapter-15 full.

R/32
18/01/2022, 19/01/2022, 21/01/2022

Ch-15 Data Handling

( Download Ch-15 in pdf by clicking on the chapter's name above.)

TOPIC

Understand the use of organising data

Use tally marks to organise data

Represent data through pictographs and bargraphs

EXPLAINED

Understand the use of organising data

Use tally marks to organise data

Represent data through pictographs and bargraphs

MUST WATCH FOR BETTER UNDERSTANDING

Video-01 Introduction ( Data Handling )

Video-02 Pictograph

Video-03 Bar Graph

Main Teachings

Oral Explanation Online with some written work.

Introduction

Data is a collection of numbers gathered to give some information. To get particular information from the given data quickly, the data has to be organized first.

The organization of data can be done in various ways. One way to organize data is by using tally marks. Tally marks are a way of expressing numbers in groups of 5. The numbers are represented as follows:
Another way of organizing data is through the use of pictographs. A pictograph represents data through pictures of objects. It helps answer the questions on the data at a glance. For e.g. the following table shows the no of apples sold by a vendor during a week:
Maximum number of apples were sold on Monday that is, 50 apples since there are 5 pictures. On Wednesday, no apples were sold as there is no picture.
The following examples illustrate the use of above methods:

Problem: Following is the choice of sweets of 30 students of Class VI.
Ladoo, Barfi, Ladoo, Jalebi, Ladoo, Rasgulla, Jalebi, Ladoo, Barfi, Rasgulla, Ladoo, Jalebi, Jalebi, Rasgulla, Ladoo, Rasgulla, Jalebi, Ladoo, Rasgulla, Ladoo, Ladoo, Barfi, Rasgulla, Rasgulla, Jalebi, Rasgulla, Ladoo, Rasgulla, Jalebi, Ladoo.
Arrange the names of sweets in a table using tally marks.
Which sweet is preferred by most of the students?
Ladoo is most preferred by people as 11 people prefer it.

Problem: The number of girl students in each class of a co-educational middle school is depicted by the pictograph:
Observe this pictograph and answer the following questions:
(a) Which class has the minimum number of girl students?
(b) Is the number of girls in Class VI less than the number of girls in Class V?
(c) How many girls are there in Class VII?

Solution:
Class 8 has minimum number of girls. It has more than 4 but less than 8 girls.
No, class 6 has 16 girls (4×4) while class 5 has less than 16.
Class 7 is represented by 3 pictures. Thus, it has 3×4 = 12 girls.

BAR GRAPH
Bar graphs are the pictorial representation of data (generally grouped), in the form of vertical or horizontal rectangular bars, where the length of bars are proportional to the measure of data. They are also known as bar charts. Bar graphs are one of the means of data handling in statistics.
The collection, presentation, analysis, organization, and interpretation of observations of data are known as statistics. The statistical data can be represented by various methods such as tables, bar graphs, pie charts, histograms, frequency polygons, etc. In this article, let us discuss what is a bar chart, different types of bar graphs, uses, and solved examples.

What is Bar Graph?
The pictorial representation of grouped data, in the form of vertical or horizontal rectangular bars, where the lengths of the bars are equivalent to the measure of data, are known as bar graphs or bar charts.
The bars drawn are of uniform width, and the variable quantity is represented on one of the axes. Also, the measure of the variable is depicted on the other axes. The heights or the lengths of the bars denote the value of the variable, and these graphs are also used to compare certain quantities. The frequency distribution tables can be easily represented using bar charts which simplify the calculations and understanding of data.

The three major attributes of bar graphs are:

The bar graph helps to compare the different sets of data among different groups easily.
It shows the relationship using two axes, in which the categories on one axis and the discrete values on the other axis.
The graph shows the major changes in data over time.
Drawing a Bar Graph
To draw a bar graph, first of all draw a horizontal line and a vertical line. On the

Horizontal line we will draw bars representing the data (numbers) and on vertical line we will write numerals .which shows what data is being represented.

Same data can also be represented by interchanging the items on horizontal and vertical axis.
It is important to take bars of same width keeping uniform gap between them. Next, a scale is chosen if needed. The scale varies according to the data given.
Following problems explain how a bar graph is drawn:

Problem: The number of Mathematics books sold by a shopkeeper on six consecutive days is shown below:
Draw a bar graph to represent the above information choosing the scale of your choice.
Solution:
To draw a bar graph, days are taken on horizontal axis and the number of books sold is taken on the vertical axis.
The scale taken for representing this data is 1 unit length = 5 shirts. This scale is taken along the vertical line since the number of books is marked on the y axis.
The height of the bars for various days is:
Problem: Observe this bar graph which shows the marks obtained by Aziz in half-yearly examination in different subjects. Answer the given questions.
(a) What information does the bar graph give?
(b) Name the subject in which Aziz scored maximum marks.
(c) Name the subject in which he has scored minimum marks.
(d) State the name of the subjects and marks obtained in each of them.

Solutions:
(a) The bar graph shows the marks scored by Aziz in different subjects.
(b) Aziz scored maximum marks in Hindi i.e 80 marks
(c) Aziz scored minimum marks in Social Studies i.e 40 marks
(d) Hindi – 80 marks English – 60 marks Mathematics – 70 marks

Science – 50 marks Social Studies – 40 marks

Problem: Following table shows the number of bicycles manufactured in a factory during the years 1998 to 2002. Illustrate this data using a bar graph. Choose a scale of your choice.
(a) In which year were the maximum number of bicycles manufactured?
(b) In which year were the minimum number of bicycles manufactured?

Solutions:
By taking a scale of 1 unit length = 100 bicycles we may draw a bar graph of above data as follows.
(a) In the year 2002, maximum number of bicycles were manufactured i.e 1200 bicycles
(b) In the year 1999, minimum number of bicycles were manufactured i.e 600 bicycles.

ASSIGNMENTS
Do Chapter-15 all exercises and Chapter Test.

R/31
11/01/2022, 12/01/2022
ASSIGNMENTS
Revise Chapter-6 all exercises.

R/30
20/12/2021, 22/12/2021

Chapter-6 Decimals

( Download Ch-6 in pdf by clicking on the chapter's name above.)

TOPIC

Understand the concept of decimals

Represent decimals on a number line

Find the place value of decimals

Read and write decimals

Define like and unlike decimals

Compare and order Decimals

Convert a decimal into a fraction

Convert a fraction into a decimal

Use decimals in representing money (rupees and paise) and metric measures-metre, centimetre, kilometre, kilogram, litre, millilitre, etc.

Add and Subtract decimals

EXPLAINED

Understand the concept of decimals

Represent decimals on a number line

Find the place value of decimals

Read and write decimals

Define like and unlike decimals

Compare and order Decimals

Convert a decimal into a fraction

Convert a fraction into a decimal

Use decimals in representing money (rupees and paise) and metric measures-metre, centimetre, kilometre, kilogram, litre, millilitre, etc.

Add and Subtract decimals

MUST WATCH FOR BETTER UNDERSTANDING

Video-1 Understand the concept of decimals

Video-2 Representing decimals on a number line

Video-3 Place value of decimals

Video-4 Reading and writing decimal numbers

Video-5 Like and Unlike decimals

Video-6 Comparing decimals

Video-7 Ordering decimals

Video-8 Conversion of decimals to fractions

Video-9 Conversion a fraction into a decimal

Video-10 Using decimal numbers

Video-11 Adding Decimals

Video-12 Subtracting Decimals

Main Teachings

Oral Explanation Online with some written work.

Decimals

When we use dots to write some numbers then that dot is the decimal point. This is used to show the part of a whole number.

Tenths

As we know that 1 cm = 10 mm, so if we have to find the opposite then

1mm = 1/10 cm or one-tenth cm or 0.1 cm.

Hence, the first number after the decimal represents the tenth part of the whole

This reads as “thirty-four point seven”.

Representation of Decimals on Number Line

To represent decimals on the number line we have to divide the gap of each number into 10 equal parts as the decimal shows the tenth part of the number.

Example

Show 0.3, 0.5 and 0.8 on the number line.

Solution

All the three numbers are greater than 0 and less than 1.so we have to make a number line with 0 and 1 and divide the gap into 10 equal parts.

Then mark as shown below.

Representation of Decimals on Number Line

Fractions as Decimals

It is easy to write the fractions with 10 as the denominator in decimal form but if the denominator is not 10 then we have to find the equivalent fraction with denominator 10.

Example

Convert 12/5 and 3/2 in decimal form.

Solution

Decimals as Fractions

Example

Write 2.5 in a fraction.

Solution

Hundredths

As we know that 1 m = 100 cm, so if we have to find the opposite then

1 cm = 1/100 m or one-hundredth m or 0.01 m.

Hence, the second numbers after the decimal represent the hundredth part of the whole.

It reads as “thirteen point nine five”.

Decimal in the hundredth form shows that we have divided the number into hundred equal parts.

Example

If we say that 25 out of 100 squares are shaded then how will we write it in fraction and decimal form?

Solution

25 is a part of 100, so the fraction will be 25/100.

In the decimal form we will write it as 0.25.

Place Value Chart

This is the place value chart which tells the place value of each digit in the decimal number. It makes it easy to write numbers in decimal form.

Example

With the given place value chart write the number in the decimal form.

Solution

According to the above table-

Comparing Decimals

1. If the whole number is different.

If the whole numbers of the decimals are different then we can easily compare them .the number with the greater whole number will be greater than the other.

Example

Compare 532.48 and 682.26.

Solution:

As the whole numbers are different, so we can easily find that the number with a greater whole number is greater.

Hence 682.26 > 532.48

2. If the whole number is the same

If the whole numbers of the decimals are same then we will compare the tenth and then the hundredth part if required.

The number with the greater tenth number is greater than the other.

Example

Compare 42.36 and 42.68.

Solution

As the whole number is the same in both the numbers so we have to compare the tenth part.

Hence 42.68 > 42.36

Using Decimals

Generally, decimals are used in money, length and weight.

1. Money

Example: 1

Write 25 paise in decimals.

Solution:

100 paise = 1 Rs.

1 paise = 1/100 Rs. = 0.01 Rs.

25 paise = 25/100 Rs. = 0.25 Rs.

Example: 2

Write 7 rupees and 35 paise in decimals.

Solution:

7 rupees is the whole number, so

7 + 35/100 = 7 + 0.35 = 7.35 Rs.

2. Length

Example

If the height of Rani is 175 cm then what will be her height in meters?

Solution

100 cm = 1 m

1 cm = 1/100 m = 0.01 m

175 cm = 175/100 m

Hence, the height of Rani is 1.75 m.

3. Weight

Example

If the weight of a rice box is 4725 gram then what will be its weight in a kilogram?

Solution

1000 gm = 1 kg

1 gm = 1/1000 kg = 0.001 kg

Addition of Decimal numbers

To add the decimal numbers we can add them as whole numbers but the decimal will remain at the same place as it was in the given numbers. It means that we have to line up the decimal point in each number while writing them, and then add them as a whole number.

Example: 1

Add 22.3 and 34.1

Solution:

Write the numbers as given below, and then add them.

Example: 2

Add 1.234 and 4.1.

Solution:

There are three numbers after decimal in one number and one number after decimal in another number. So we should not get confused and write the numbers by lining up the decimal points of both the numbers, then add them.

Subtraction of Decimal Numbers

Subtraction is also done as normal whole numbers after lining up the decimals of the given number.

Example

Subtract 243.86 from 402.10.

Solution

Write the numbers in a line so that the decimal points of both the numbers lined up.
Then subtract and borrow as we do in whole numbers.
Line up the decimal point in the answer also.

ASSIGNMENTS

Do Chapter-6 all exercises, Mental Maths, MCQs and Chapter Test.

R/29
06/12/2021, 09/12/2021

Chapter-4 INTEGERS

CHAPTER-11

THREE DIMENSIONAL SHAPES

CHAPTER-14 PERIMETER AND AREA

ASSIGNMENTS

Revise all ex's of Chapter (4 and 11) and ex's A and B of Chapter-14 for P.T.-III.

R/28
23/11/2021, 26/11/2021, 29/11/2021, 04/12/2021

Chapter-5 Fractions

(Download Ch-5 in pdf by clicking on the chapter's name above.)

TOPIC

Concept of Fractions

Represent Fractions on the number line

Types of Fractions

Equivalent Fractions

Compare Fractions

Reduce Fractions to its lowest forms

Add and Subtract Fractions

EXPLAINED

Concept of Fractions

Represent Fractions on the number line

Types of Fractions

Equivalent Fractions

Compare Fractions

Reduce Fractions to its lowest forms

Add and Subtract Fractions

MUST WATCH FOR BETTER UNDERSTANDING

Video-1 Concept of Fractions

(Introduction)

Video-2 Represent fractions on number line

Video-3 Define the types of Fractions

Video-4 Equivalent Fractions

Video-5 Compare Fractions

Video-6 Reduce fractions to lowest terms

Video-7 Addition and Subtraction of Fractions

Main Teachings

Oral Explanation Online with some written work.

ASSIGNMENTS

Do Chapter-5 all exercises, Mental Maths, MCQs and Chapter Test, page nos 108-111.

R/27
12/11/2021, 13/11/2021, 16/11/2021, 18/11/2021, 20/11/2021, 22/11/2021

Chapter-14 Perimeter and Area

(Download Ch-14 in pdf by clicking on the chapter's name above.)

TOPIC

Understand the concept of perimeter of different shapes

Perimeter of a rectangle and it's special case - square

Understand the concept of Area

Area of a rectangle and a square

EXPLAINED

Understand the concept of perimeter of different shapes

Perimeter of a rectangle and it's special case - square

Understand the concept of Area

Area of a rectangle and a square

MUST WATCH FOR BETTER UNDERSTANDING

Video-1 Understand the concept of perimeter of different shapes

Video-2 Perimeter of rectangle and square

Video-3 Understand the concept of Area

Video-4 Area of Rectangle and Square

INTRODUCTION

In this section, we shall study the Perimeter and Area for class 6^th of plane figures. The Perimeter of the plane figures is the measure related to its Boundary and the Area of the plane figures is the measure related to its region or surface occupied by it.

What are plane figures?

Plane figures are two-dimensional figures which are drawn on the plane surface.

Open Figures

In the open figures, the starting point and the ending point of the figure are not at the same point. The figures in which the starting point and the ending point are not joined, are called open figures.

Starting point – A, Ending point – B

Closed Figures

In the closed figures, the starting point and the ending point of the figure are at the same point. The figures in which the starting point and the ending point are joined, are called closed figures.

Starting point – A, Ending point – B

What is Perimeter?

Perimeter is the complete measurement of the boundary of the closed figures. The Perimeter of the closed figures can be found but not of the open figures.

In the above figures, to calculate the perimeter we start from point A and complete measurement is from point A to point A.

For figure (1), Perimeter = AB + BC + CA

For figure (2), Perimeter = AB + BC + CD + DA

For figure (3), Perimeter = AB + BC + CD + DA

The Perimeter of Irregular Shapes

Irregular shapes are the figures that have all the sides and all the angles of different measures. Such types of figures are called irregular closed figures. The Perimeter of irregular shapes is the total of all sides. Let’s understand with examples.

Example – find the perimeter of the figures given below.

Solution –

Perimeter of figure (1) = AB + BC + CD + DE + EA

= 5 cm + 3 cm + 3 cm + 5 cm + 4 cm

= 20 cm Ans.

Perimeter of figure (2) = AB + BC + CD + DE + EF + FA

= 4 cm + 6 cm + 3 cm + 5 cm + 4 cm + 3 cm

= 25 cm Ans.

The Perimeter of Regular Shapes

The figures that have all the sides and all the angles of the same measure are called Regular shapes. These types of figures are called Regular closed figures. For regular shapes, we can find the perimeter by multiplying the number of sides to the measure of each side. We can understand it by the example solved below.

Example – Find the perimeter of the figures given below.

Solution –

In figure (1), all the three sides of the triangle are equal it means this triangle is an equilateral triangle

Therefore, The Perimeter of an Equilateral Triangle = 3×Side

= 3×5 cm = 15 cm Ans.

In figure (2), all the four sides are equal so it is a square.

Therefore, The Perimeter of Square = 4×Side

= 4×6 cm = 24 cm Ans.

Note – We can make a general formula to find the perimeter of a regular shape.

The perimeter of a Regular shape = Number of sides × Measure of each side

The Perimeter of a Rectangle

We know that in a rectangle, there are four sides and the opposite sides are equal. So how can we find the perimeter of a rectangle? Let’s see.

The above figure is a rectangle ABCD. Opposite sides will be equal so AB = CD and BC = AD.

Now, perimeter of rectangle ABCD = AB + BC + CD + DA

= AB + BC + AB + BC [∵ AB = CD and BC = AD]

= 2AB + 2BC

= 2(AB + BC)

Here, AB = Length of the rectangle and BC = Breadth of the rectangle.

So, we can write as the formula, Perimeter of Rectangle = 2(Length + Breadth)

It means if we have to find the perimeter of a rectangle, we have to add length and breadth and then multiply by 2.

Example – Find the perimeter of the rectangle given below.

Solution – Perimeter of the rectangle = 2(Length + Breadth)

= 2(6 cm + 3 cm)

= 2(9 cm)

= 18 cm Ans.

Note – 1) Perimeter is a type of Distance so the unit of the perimeter is a length unit.

2) Larger the figures have a larger perimeter.

What is Area?

When we draw a closed figure, the figure covers the region which is enclosed by that. That region is known as the Area of the figure. Here are some closed figures.

All the above figures cover some amount of surface. We can see that the figure which is larger, is covering more amount of the surface. Sometimes we can’t say which figure has more area. In this condition, we use squared paper or graph paper to calculate the area. Let’s take an example.

In the squared paper, each side of every square is of the measure 1 cm. to calculate the area on squared paper, we have to keep notice some rules.

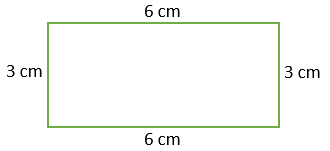
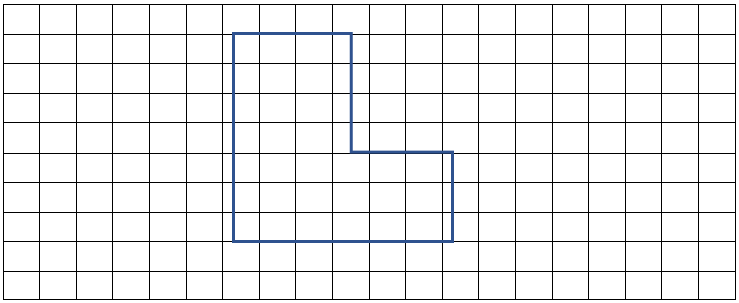
The square which is completely covered under the figure, counted as a full square.
The square which is half covered under the figure, counted as half square.
The square which is covered less than half, is not counted.
The square which is covered more than half, counted as a full square.

Now, in the above example,

Number of squares which are completely covered = 23 squares

Number of squares which are half covered = 4 = 2 full squares

Number of squares which are covered less than half = 3 squares (not counting)

Number of squares which are covered more than half = 7 squares (counting as full squares)

Therefore, the area of the given figure will be = 23 + 2 + 7

= 32 square unit

Note – We measure the area of any closed figure in a square unit. If the sides of a figure are in centimeters then the unit of the area will be square centimeter (sq. cm.).

Area of Rectangle

If we draw a Rectangle on a squared paper and calculate the area, then we shall find that the squares covered by the rectangle are equal to the multiplication of length and breadth of it.

Squares covered by the Rectangle = 24 squares

Multiplication of length and breadth = 6×4 = 24

Since squares covered by the rectangle and the multiplication of length and breadth are equal.

So, we can calculate the area of a rectangle by multiplying the length and breadth of the rectangle.

Therefore, Area of Rectangle = Length × Breadth

Example – If the length and breadth of a rectangular table are 10 cm and 7 cm respectively, then find the area of the table.

Solution – here, length of table = 10 cm

Breadth of table = 7 cm

So, area of rectangular table = length × breadth

= 10 cm × 7 cm

= 70 square cm. Ans.

Area of a Square

The Area of the square can be found the same as the area of the rectangle. We know that if the length and breadth of a rectangle are the same then that will be a square.

Squares covered by the square = 16 squares

Multiplication of its two sides = 4×4 =16

Since both, the values are the same so we can calculate the area of a square by multiplying its two sides.

Therefore, Area of Square = Side × Side

Example – Find the area of a square-shaped tile, if each side is 5 cm.

Solution – Each side of a square-shaped tile = 5 cm

So, area of a square-shaped tile = side × side

= 5 cm × 5 cm

= 25 sq. cm. Ans.

ASSIGNMENTS

Do Chapter-14 all exercises, Mental Maths, MCQs and Chapter Test page nos 241-243.

R/26
01/11/2021, 03/11/2021

Chapter-11 Three Dimensional Shapes

(Download Ch-11 in pdf by clicking on the chapter's name above.)

TOPIC

Identify various 3D shapes

Understand the elements of 3D figures ( types of surfaces,faces, edges and corners )

Draw the nets of 3D shapes

EXPLAINED

Identify various 3D shapes

Understand the elements of 3D figures ( types of surfaces,faces, edges and corners )

Draw the nets of 3D shapes

MUST WATCH FOR BETTER UNDERSTANDING

Video-1 2D and 3D shapes

Video-2 Nets of Solids

Video-3 Understand the elements of of 3D figures

What are Three-Dimensional shapes?

In geometry, a three-dimensional shape can be defined as a solid figure or an object or shape that has three dimensions – length, width and height. Unlike two-dimensional shapes, three-dimensional shapes have thickness or depth.

The attributes of a three-dimensional figure are faces, edges and vertices. The three dimensions compose the edges of a 3D geometric shape.

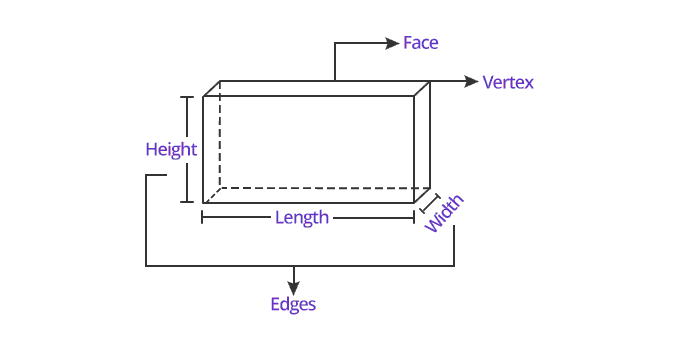
Three dimensions of a three-dimensional shape or 3d Figure

A cube, rectangular prism, sphere, cone and cylinder are the basic 3-dimensional shapes we see around us.

Three-dimensional 3-D shapes cube rectangular prism cuboid cone cylinder sphere

We can see a cube in a Rubik’s cube and a die, a rectangular prism in a book and a box, a sphere in a globe and a ball, a cone in carrot and an ice cream cone and a cylinder in a bucket and a barrel, around us.

Three-dimensional 3-D shapes figures real life examples around us

Here’s a list of the 3-D or three-dimensional shapes with their name, pictures and attributes.

Name of 3D shape:	Picture of 3D shape:	Attributes:
Cube		Faces - 6 Edges - 12 Vertices - 8
Rectangular Prism or Cuboid		Faces - 6 Edges - 12 Vertices - 8
Sphere		Curved Face - 1 Edges - 0 Vertices - 0
Cone		Flat Face - 1 Curved Face - 1 Edges - 1 Vertices - 1
Cylinder		Flat Face - 2 Curved Face - 1 Edges - 2 Vertices - 0

Fun Facts

All three-dimensional shapes are made up of two-dimensional shapes.

Pyramid

A pyramid is a polyhedron with a polygon base and an apex with straight edges and flat faces. Based on their apex alignment with the center of the base, they can be classified into regular and oblique pyramids. A pyramid with:

A triangular base is called a Tetrahedron
A quadrilateral base is called a square pyramid
A pentagon base is called a pentagonal pyramid
A regular hexagon base is called a hexagonal pyramid

Prisms

Prisms are solids with identical polygon ends and flat parallelogram sides. Some of the characteristics of a prism are:

It has the same cross-section all along its length.
The different types of prisms are - triangular prisms, square prisms, pentagonal prisms, hexagonal prisms, etc.
Prisms are also broadly classified into regular prisms and oblique prisms.

ASSIGNMENTS

Do Chapter-11 all exercises, Mental Maths, MCQs and Chapter test page nos 211-213.

R/25
26/10/2021, 30/10/2021

Chapter-4 Integers

(Download Ch-4 in pdf by clicking on the chapter's name above.)

TOPIC

Understand the need of negative numbers

Understand the oppositeness in daily life situations- representation by positive and negative integers

Represent integers on a number line

Compare and arrange the integers in ascending or descending order

Find the absolute value of an integer

Add and Subtract integers

EXPLAINED

Understand the need of negative numbers

Understand the oppositeness in daily life situations- representation by positive and negative integers

Represent integers on a number line

Compare and arrange the integers in ascending or descending order

Find the absolute value of an integer

Add and Subtract integers

MUST WATCH FOR BETTER UNDERSTANDING

Video-1 Integers

Video-2 Representation of integers on number line

Video-3 What is absolute value?

Video-4 Operation of negative numbers without using number lines

Video-5 Addition and Subtraction of Integers

Main Teachings

Oral Explanation Online with some written work.

What Is an Integer?

An integer is a number with no decimal or fractional part, from the set of negative and positive numbers, including zero. Examples of integers are: -5, 0, 1, 5, 8, 97, and 3,043.

A set of integers, which is represented as Z, includes:

Positive Integers: An integer is positive if it is greater than zero. Example: 1, 2, 3 . . .
Negative Integers: An integer is negative if it is less than zero. Example: -1, -2, -3 . . .
Zero is defined as neither negative nor positive integer. It is a whole number.

Z = {... -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, ...}

Integers on a Number Line

A number line is a visual representation of numbers on a straight line. This line is used for the comparison of numbers that are placed at equal intervals on an infinite line that extends on both sides, horizontally.

Just like other numbers, the set of integers can also be represented on a number line.

Graphing Integers on a Number Line

The number on the right horizontal side is always greater than the left side number.
Positive numbers are placed on the right side of 0, as they are greater than “0”.
Negative numbers are placed on the left side of “0”, as they are smaller than “0”.
Zero, which isn't positive or negative, is kept at the center.

Integer Operations

The four basic arithmetic operations associated with integers are:

Addition of Integers
Subtraction of Integer
Multiplication of Integers
Division of Integers

There are some rules for doing these operations.

Before we start learning these methods of integer operations, we need to remember a few things.

If there is no sign in front of a number, it means that the number is positive. For example, 5 means +5.

The absolute value of an integer is a positive number, i.e., |−2| = 2 and |2| = 2.

Addition of Integers

While adding two integers, we come across the following cases:

Both integers have the same signs: Add the absolute values of integers, and give the same sign as that of the given integers to the result.
One integer is positive and the other is negative: Find the difference of the absolute values of the numbers and then give the original sign of the larger of these numbers to the result.

Example 1:

Adding two integers: Calculate the value of 2 + (-5).

Solution:

Here, the absolute values of 2 and (-5) are 2 and 5 respectively.

Their difference (larger number - smaller number) is 5 - 2 = 3

Now, among 2 and 5, 5 is the larger number and its original sign “-”.

Hence, the result gets a negative sign, "-”.

Therefore, 2 + (-5) = -3

Example 2:

Adding two integers: Calculate the value of -2 + 5.

Solution:

Here, the absolute values of (-2) and 5 are 2 and 5 respectively.

Their difference (larger number - smaller number) is 5 - 2 = 3

Now, among 2 and 5, 5 is the larger number and its original sign “+”.

Hence, the result will be a positive value.

Therefore,(-2) + 5 = 3

We can also solve the above problem using a number line. The rules for the addition of integers on the number line are:

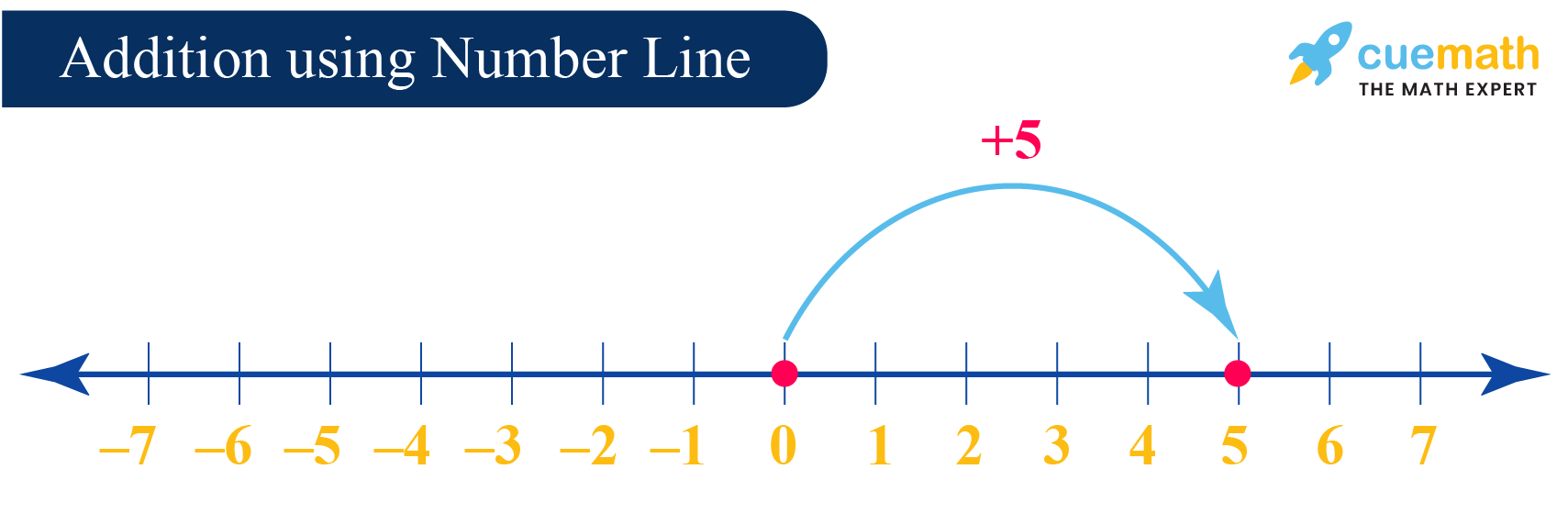
always start from "0".
move to the right side, if the number is positive.
move to the left side, if the number is negative.

Let's find the value of 5 + (-10) using a number line.

In the given problem, the first number is 5 which is positive.

So, we start from 0 and move 5 units to the right side.

Addition of Integers: Adding integers using the number line

The next number in the given problem is -10, which is negative.

We move (from the fifth unit) 10 units to the left side.

The number we have moved to finally is -5.

Subtraction of Integers

To carry out the subtraction of two integers:

Convert the operation into an addition problem by changing the sign of the subtrahend.
Apply the same rules of addition of integers and solve the problem thus obtained in the above step.

Example:

Subtracting two integers: Calculate the value of 7 - 10.

Solution:

Converting the given expression into an addition problem, we get: 7 + (-10).

Now, the rules for this operation will be the same as for the addition of two integers.
Here, the absolute values of 7 and (-10) are 7 and 10 respectively.
Their difference (larger number - smaller number) is 10 - 7 = 3.
Now, among 7 and 10, 10 is the larger number and its original sign “-”.
Hence, the result gets a negative sign, "-”.
Therefore, 7 - 10 = -3

Ordering of Integers

Ordering of integers is stated for the series or a sequence where numbers are arranged in an order. The integers are ordered on a number line based on positive integers and negative integers. The integers that are greater than 0 are positive integers and integers less than 0 are negative integers.

As we know, the arrangement of numbers can be done in two ways:

Ascending order
Descending order

In ascending order, the integers are arranged from smallest to largest value whereas in descending order the integers are arranged from largest to smallest value.

Ordering of Integers on Number Line

As we have already learned, the integers are represented on a number line. The center of the number line is marked as 0. On the left side of 0, the negative integers are arranged in ascending order from left to right. On the right side of 0, the positive integers are arranged in ascending order from left to right. Thus, we can conclude that, on both sides of the 0, the integers are arranged in ascending order on the number line.

In the above figure, we can see, the integers from -6 to -1, are arranged in ascending order from left to right and the integers from +1 to +6 are arranged in ascending order from left to right. So basically, all the integers from -6 to +6, are in ascending order from left to right whereas integers from right to left (+6 to -6) are in descending order.

Hence, we can say, -6 is smaller than all the integers marked on the number line (in the above figure) whereas 6 is the greatest of the integers.

Therefore, we can order the integers as:

-6 < -5 < -4 < -3 < -2 < -1 < 0 < 1 < 2 < 3 < 4 < 5 < 6

Facts:

Order of Integers on left side of the number line are smaller than 0 and order of integers on the right side of the number line are greater than 0
The more the integer is negative, the more its value is smaller
The more the integer is positive, the more its value is greater
Zero is neither a negative integer nor a positive integer
All positive integers are greater than all the negative integers

Comparing Integers

One integer can be either greater or smaller than another integer. Thus, to compare two integers we use symbols greater than (>) and less than (<). Also, if two integers are equal to each other then we use the ‘equal to’ (=) symbol. See the examples below:

0 > – 8
8 > – 5
0 < 3
-1 > -10
10 < 12
-20 < 1
-100 < -10
100 > -200

From the above examples, we can observe that, the more an integer is negative, the less its value is.

ASSIGNMENTS

Do Chapter-4 all ex's, Mental Maths, Multiple choice questions and Chapter test page nos 86-87.

R/24
06/10/2021, 09/10/2021, 18/10/2021

Revision of Chapter-9 (Basic Geometric Figures) and Chapter-10 (Plane Figures)

ASSIGNMENTS

Revise Chapter-9 and 10 all exercises + MCQS, Mental Maths and Chapter Test.V

R/23

29/09/2021, 01/10/2021, 04/10/2021, 05/10/2021

REVISION

Ratio
If we compare two quantities using division then it is called ratio. It compares quantities in terms of ‘How many times’. The symbol to represent ratio is “:”.
It reads as “4 is to 3”
It can also be written as 4/3.
Example
If there are 35 boys and 25 girls in a class, then what is the ratio of
Number of boys to total students
Number of girls to total students.
Solution
In the ratio, we want the total number of students.
Total number of students = Number of boys + Number of girls
35 + 25 = 60
Ratio of number of boys to total number of students
The ratio of the number of girls to the total number of students
The unit must be same to compare two quantities
If we have to compare two quantities with different units then we need to convert them in the same unit .then only they can be compared using ratio.
Example
What is the ratio of the height of Raman and Radha if the height of Raman is 175 cm and Radha is 1.35 m?
Solution
The unit of the height of Raman and Radha is not same so convert them in the same unit.
Height of Radha is 1.35 m = 1.35 × 100 cm = 135 cm
The ratio of the height of Raman and Radha
The Lowest form of the Ratio
If there is no common factor of numerator and denominator except one then it is the lowest form of the ratio.
Example
Find the lowest form of the ratio 25: 100.
Solution
The common factor of 25 and 100 is 25, so divide both the numerator and denominator with 25.
Hence the lowest ratio of 25: 100 is 1: 4.
Proportion
If we say that two ratios are equal then it is called Proportion.

We write it as a: b : : c: d or a: b = c: d
And reads as “a is to b as c is to d”.
Example
If a man runs at a speed of 20 km in 2 hours then with the same speed would he be able to cross 40 km in 4 hours?
Solution
Here the ratio of the distances given is 20/40 = 1/2 = 1: 2
And the ratio of the time taken by them is also 2/4 = 1/2 = 1: 2
Hence the four numbers are in proportion.
We can write them in proportion as 20: 40 : : 2: 4
And reads as “20 is to 40 as 2 is to 4”.
Extreme Terms and Middle Terms of Proportion
The first and the fourth term in the proportion are called extreme terms and the second and third terms are called the Middle or the Mean Terms.
In this statement of proportion, the four terms which we have written in order are called the Respective Terms.
If the two ratios are not equal then these are not in proportion.
Example 1
Check whether the terms 30,99,20,66 are in proportion or not.
Solution 1.1
To check the numbers are in proportion or not we have to equate the ratios.
As both the ratios are equal so the four terms are in proportion.
30: 99 :: 20: 66
Unitary Method
If we find the value of one unit then calculate the value of the required number of units then this method is called the Unitary method.
Example 1
If the cost of 3 books is 320 Rs. then what will be the cost of 6 books?
Solution 1
Cost of 3 books = Rs. 320
Cost of 1 book = 320/3 Rs.
Cost of 6 books = (320/3) × 6 = 640 Rs.
Hence, the cost of 6 books is Rs. 640.
ASSIGNMENTS

Revise Chapter-8 all exercises.

R/22

24/09/2021, 25/09/2021, 28/09/2021

REVISION

A number is a mathematical value used to count and measure different objects. With the help of the numbers we all are able to add, subtract, divide and multiple. Here we will be learning how to compare numbers, expand the number and also learn about the largest and the smallest numbers.
What are Natural numbers?
Counting numbers 1, 2, 3, 4, ...... etc. are called Natural numbers. The smallest natural number is 1 and there is no largest natural number.

Roman numerals and the Hindu-Arabic numeral system are the two different types of number system used for writing numbers in many places. We all can see the roman numerals in clocks, page numbers, school timetable in syllabus page, etc.

Introduction

Introduction to numbers

Numbers are arithmetic values.
Numbers are used to convey the magnitude of everything around us.

Comparing numbers

Comparing numbers when the total number of digits is different

The number with most number of digits is the largest number by magnitude and the number with least number of digits is the smallest number.
Example: Consider numbers: 22, 123, 9, 345, 3005. The largest number is 3005 (4 digits) and the smallest number is 9 (only 1 digit)

Comparing numbers when the total number of digits is same

The number with highest leftmost digit is the largest number. If this digit also happens to be the same, we look at the next leftmost digit and so on.
Example: 340, 347, 560, 280, 265. The largest number is 560 (leftmost digit is 5) and the smallest number is 265 (on comparing 265 and 280, 6 is less than 8).

Ascending and Descending Order and Shifting Digits

Ascending order and Descending order

Ascending Order: Arranging numbers from the smallest to the greatest.
Descending Order: Arranging numbers from the greatest to the smallest number.
Example: Consider a group of numbers: 32, 12, 90, 433, 9999 and 109020.
They can be arranged in descending order as 109020, 9999, 433, 90, 32 and 12, and in ascending order as 12, 32, 90, 433, 9999 and 109020.

How many numbers can be formed using a certain number of digits?

If a certain number of digits are given, we can make different numbers having the same number of digits by interchanging positions of digits.
Example: Consider 4 digits: 3, 0, 9, 6. Using these four digits,
(i) Largest number possible = 9630
(ii) Smallest number possible = 3069 (Since 4 digit number cannot have 0 as the leftmost number, as the number then will become a 3 digit number)

Shifting digits

Changing the position of digits in a number, changes magnitude of the number.
Example: Consider a number 789. If we swap the hundredths place digit with the digit at units place, we will get 987 which is greater than 789.
Similarly, if we exchange the tenths place with the units place, we get 798, which is greater than 789.

Place value

Each place in a number, has a value of 10 times the place to its right.
Example: Consider number 789.
(i) Place value of 7 = 700
(ii) Place value of 8 = 80
(iii) Place value of 9 = 9
Larger Numbers and Estimates
Introducing large numbers
Large numbers can be easily represented using the place value. It goes in the ascending order as shown below
8 digits
7 digits 6 digits 5 digits 4 digits 3 digits
10 million
(1 crore)
1 million
(10 lakhs)
Hundred Thousands
(1 lakh)
Ten Thousands Thousands
Hundreds
- Largest 3 digit number + 1 = Smallest 4 digit number.
- Largest 4 digit number + 1 = Smallest 5 digit number, and so on.
  Example: 9999 (greatest 4 digit number) + 1 = 10,000 (smallest 5 digit number)
- We can convert every large numbers in terms of smaller numbers:
  Remember, 1 hundred = 10 tens
  1 thousand = 10 hundreds = 100 tens
  1 lakh = 100 thousands = 1000 thousands
  1 crore = 100 lakhs = 10,000 thousands

Estimation

When there is a very large figure, we approximate that number to the nearest plausible value. This is called estimation.
Estimating depends on the degree of accuracy required and how quickly the estimate is needed.
Example:
Given Number Appropriate to Nearest Rounded Form
75847 Tens 75850
75847 Hundreds 75800
75847 Thousands 76000
75847 Tenth thousands 80000

Estimating sum or difference

Estimations are used in adding and subtracting numbers.

Example of estimation in addition: Estimate 7890 + 437.
Here 7890 > 437.
Therefore, round off to hundreds.
7890 is rounded off to 7900
437 is rounded off to + 400
Estimated Sum = 8300
Actual Sum = 8327
Example of estimation in subtraction: Estimate 5678 – 1090.
Here 5678 > 1090.
Therefore, round off to thousands.
5678 is rounded off to 6000
1090 is rounded off to – 1000
Estimated Difference = 5000
Actual Difference = 4588

Estimating products of numbers

Round off each factor to its greatest place, then multiply the rounded off factors.
Estimating the product of 199 and 31:
199 is rounded off to 200
31 is rounded off to 30
Estimated Product = 200 $\times$ 30 = 6000
Actual Result = 199 $\times$ 31 = 6169

BODMAS

We follow an order to carry out mathematical operations. It is called as BODMAS rule.

While solving mathematical expressions, parts inside a bracket are always done first, followed by of, then division, and so on.

Example :

[(5 + 1) × 2] ÷ (2 × 3) + 2 – 2 = ?

[(5 + 1) × 2] ÷ (2 × 2) + 2 – 2….{Solve everything which is inside the brackets}

= [6 × 2] ÷ 6 + 2 – 2…..{Multiplication inside brackets}

= 12 ÷ 6 + 2 – 2……{Division}

= 2 + 2 – 2……{Addition}

= 4 – 2…….{Subtraction}

= 2

Using brackets

Using brackets can simplify mathematical calculations.
Example :

7 × 109 = 7 × (100 + 9) = 7 × 100 + 7 × 9 = 700 + 63 = 763
7 × 100 + 6 × 100 = 100 × (7 + 6) = 100 × 13 = 1300
Introducing Large Numbers

What is the Indian Numeral System?
The Indian numeral system contains numerals that are used to represent the numbers using a set of symbols. This system can be distinguished from the other numeral systems based on the nomenclature followed for different place values. When we use the Indian numeral system, we count with ones, tens, hundreds, thousands, ten thousands, lakhs, ten lakhs, and crores.
The following table depicts the different periods and places according to the number of digits in a number.
Use of Commas
According to the Indian numeral system, separators (comma) are used after every period while representing a number in its standard numeral form. For example, the number 384756182 can be better represented as 38,47,56,182 in the standard Indian numeral system form using separators after every period.
The number name for 38,47,56,182 is written as thirty-eight crore, forty-seven lakh fifty-six thousand, one hundred and eighty-two.
Place value and face value:
The place value of a digit of a number depends upon its position in the number. The face value of a digit of a number does not depend upon its position in the number. It always remains the same wherever it lies regardless of the place it occupies in the number.
Example: Let us see the place value and face value of the underlined digit in the number 1,32,460. The digit 2 in the number 1,32,460 lies in the thousands period (1000) and hence the place value of 2 is 2 thousands (or 2000). The face value of 2 is 2 only.
Expanded form:
When a number is written as the sum of the place values of all the digits of the number, then the number is in its expanded form.
Example: The expanded form of 9,67,480 is as shown below:
9,67,480 = 900000 + 60000 + 7000+400+80.

International system of numeration
Values of the places in the International system of numeration are Ones, Tens, Hundreds, Thousands, Ten thousands, Hundred thousands, Millions, Ten millions and so on.
1 million = 1000 thousands,
1 billion = 1000 millions

Following place value chart can be used to identify the digit in any place in the International system.

Periods

Billions

Millions

Thousands

Ones

Places

Hundreds

Tens

Ones

Hundreds

Tens

Ones

Hundreds

Tens

Ones

Hundreds

Tens

Ones

Commas in International system of Numeration
As per International numeration system, the first comma is placed after the hundreds place. Commas are then placed after every three digits.
e.g. (i) 8,876,547
The number can be read as eight million eight hundred seventy-six thousand five hundred and forty-seven.

Roman Numerals
- Digits 09 in Roman are represented as : I, II, III, IV, V, VI, VII, VIII, IX, X
- Some other Roman numbers are : I = 1, V = 5 , X = 10 , L = 50 , C = 100 , D = 500 , M = 1000
Rules for writing Roman numerals
- If a symbol is repeated, its value is added as many times as it occurs.
  Example: XX = 10 + 10 = 20
- A symbol is not repeated more than three times. But the symbols X, L and D are never repeated.
- If a symbol of smaller value is written to the right of a symbol of greater value, its value gets added to the value of greater symbol.
  Example: VII = 5 + 2 = 7
- If a symbol of smaller value is written to the left of a symbol of greater value, its value is subtracted from the value of greater symbol.
  Example: IX = 10 – 1 = 9.
- Some examples : 105 = CV , 73 = LXXIII and 192 = 100 + 90 + 2 = C XC II = CXCII

ASSIGNMENTS

Revise Chapter-01 all ex's + Mental Maths, MCQs and Chapter Test.

R/21

23/09/2021
Ch-7 Algebra
Introduction to Algebra

There are so many branches of mathematics-

The study of numbers is called Arithmetic.
The study of shapes is called Geometry.
The study to use the letters and symbols in mathematics is called Algebra.

Algebra
Algebra is a part of mathematics in which the letter and symbols are used to represent numbers in equations. It helps us to study about unknown quantities.

Matchstick Patterns

No. of matchsticks used to make 1^st square = 4

No. of matchsticks used to make 2^nd square = 7

No. of matchsticks used to make 3^rd square = 10

So, the pattern that we observe here is 3n + 1

With this pattern, we can easily find the number of matchsticks required in any number of squares.

Example

How many matchsticks will be used in the 50^th figure?

Solution

3n + 1

3 × 50 + 1

= 151 matchsticks

The Idea of a Variable

Variable refers to the unknown quantities that can change or vary and are represented using the lowercase letter of the English alphabets.

One such example of the same is the rule that we used in the matchstick pattern

3n + 1

Here the value of n is unknown and it can vary from time to time.

More Examples of Variables

We can use any letter as a variable, but only lowercase English alphabets.
Numbers cannot be used for the variable as they have a fixed value.
They can also help in solving some other problems.

Example: 1

Karan wanted to buy story books from a bookstall. She wanted to buy 3 books for herself, 2 for her brother and 4 for 2 of her friends. Each book cost Rs.15.how much money she should pay to the shopkeeper?

Solution: 1

Cost of 1 book = Rs.15

We need to find the cost of 9 books.

No. of notebooks	1	2	3	4	…….	a	….....
Total cost	15	30	45	60	……	15 a

In the current situation, a (it’s a variable) stands for 9
Therefore,
Cost of 9 books = 15 × 9
= 135
Therefore Karan needs to pay Rs.135 to the shopkeeper of the bookstall.
The variable and constant not only multiply with each other but also can be added or subtracted, based on the situation.

Equation
If we use the equal sign between two expressions then they form an equation.
An equation satisfies only for a particular value of the variable.
The equal sign says that the LHS is equal to the RHS and the value of a variable which makes them equal is the only solution of that equation.
Example
3 + 2x = 13
5m – 7 = 3
p/6 = 18
If there is the greater then or less than sign instead of the equal sign then that statement is not an equation.
Some examples which are not an equation
23 + 6x > 8
6f – 3 < 24
The Solution of an Equation
The value of the variable which satisfies the equation is the solution to that equation. To check whether the particular value is the solution or not, we have to check that the LHS must be equal to the RHS with that value of the variable.
Trial and Error Method
To find the solution of the equation, we use the trial and error method.
Example
Find the value of x in the equation 25 – x = 15.
Solution
Here we have to check for some values which we feel can be the solution by putting the value of the variable x and check for LHS = RHS.
Let’s take x = 5
25 – 5 = 15
20 ≠ 15
So x = 5 is not the solution of that equation.
Let’s take x = 10
25 – 10 = 15
15 = 15
LHS = RHS
Hence, x = 10 is the solution of that equation.
ASSIGNMENTS
Revise Chapter-7 all exercises.

R/20

21/09/2021

REVISION

Chapter-2 Whole Numbers

ASSIGNMENTS

Revise Chapter-2 all exercises.

R/19

14/09/2021, 16/09/2021

REVISION

Chapter- 3 Playing with Numbers

ASSIGNMENTS

Revise Chapter-3 all exercises.

R/18

31/08/2021, 02/09/2021, 03/09/2021, 07/09/2021, 09/09/2021

Chapter- 3 Playing with Numbers

(Download Ch-3 in pdf by clicking on the chapter's name above.)

TOPICS
Factors and Multiples
Prime and Composite Numbers, even and odd numbers
Divisibility Rules
Prime Factorisation
HCF and LCM
Relation between HCF and LCM of two numbers
Concepts of HCF and LCM in solving problems based on real life situations

EXPLAINED
Factors and Multiples
Prime and Composite Numbers, even and odd numbers
Divisibility Rules
Prime Factorisation
HCF and LCM
Relation between HCF and LCM of two numbers
Concepts of HCF and LCM in solving problems based on real life situations

MUST WATCH FOR BETTER UNDERSTANDING
Video-1 Factors and Multiples
Video-2 Types of Numbers
Video-3 Divisibility Rules
Video-4 Prime Factorisation
Video-5 HCF and LCM
Video-6 Relationship between HCF and LCM
Video-7 Word Problems on HCF and LCM
Main Teachings
Oral Explanation Online with some written work.

What are Factors?
A factor of a number is an exact divisor of that number
Example
1. Factor of 6
1-> Since 1 exactly divides 6
2 -> Since it exactly divides 6
3 -> Since it exactly divides 6
6-> Since it exactly divides 6

Properties of factors

1. 1 is a factor of every number
2. every number is a factor of itself.
3. every factor of a number is an exact divisor of that number
4. every factor is less than or equal to the given number
5. number of factors of a given number are finite.

Multiple

Multiple of a number is the numbers obtained by multiplying that numbers with various Natural Numbers.
Example
Number is 6
Multiple will be
$6 \times 1 = 6$
$6 \times 2 = 12$
$6 \times 3 = 18$

Properties of Multiple

1. Every multiple of a number is greater than or equal to that number.
2. number of multiples of a given number is infinite
3. every number is a multiple of itself

Perfect Number

A number for which sum of all its factors is equal to twice the number is called a perfect number.

Example
1. 6
The factors of 6 are 1, 2, 3 and 6.
Now, $1 + 2 + 3 + 6 = 12 = 2 \times 6$ .
2. 28
All the factors of 28 are 1, 2, 4, 7, 14 and 28.
Now, $1 + 2 + 4 + 7 + 14 + 28 = 56 = 2 \times 28$ .

Prime Numbers

The numbers other than 1 whose only factors are 1 and the number itself are called Prime numbers.
Example:
2, 3, 5, 7, 11 ,13
We can find list of prime numbers till 100 using Sieve of Eratosthenes method
Step 1: Cross out 1 because it is not a prime number.
Step 2: Encircle 2, cross out all the multiples of 2, other than 2 itself, i.e. 4, 6, 8 and so on.
Step 3: You will find that the next uncrossed number is 3. Encircle 3 and cross out all the multiples of 3, other than 3 itself.
Step 4: The next uncrossed number is 5. Encircle 5 and cross out all the multiples of 5 other than 5 itself.
Step 5: Continue this process till all the numbers in the list are either encircled or crossed out.
All the encircled numbers are prime numbers. All the crossed-out numbers, other than 1 are composite numbers

Composite Numbers

Numbers having more than two factors (1 and itself) are called Composite numbers
Example:
4, 6, 8 ,9….

Even Numbers

The numbers which are multiple of 2 are called even numbers
Example
2,4,6,8,10,12,14
Even numbers have 0,2,4,6,8 in it one’s place.

Odd Numbers

The numbers which are not multiple of 2 are called odd numbers
Example
1,3, 5,7,9,11......
Important points about prime numbers based on definition of odd and even numbers
1. 2 is the smallest prime number which is even.
2. every prime number except 2 is odd.

Tests for Divisibility of Numbers

Number	Test of divisibility
2	A number is divisible by 2 if it has any of the digits 0, 2, 4, 6 or 8 in its one’s place
3	A number is divisible by 3 if the sum of the digits is a multiple of 3, then the number is divisible by 3. Example 153 - Sum of digit = 1+5+3=9 and 9 /3 =3 So, 153 is divisible by 3
4	1) For one and two-digit number, just check the divisibility by actual division. 2) For number with 3 or more digits is divisible by 4 if the number formed by its last two digits (i.e. ones and tens) is divisible by 4.
5	A number is divisible by 5 if a number which has either 0 or 5 in its one’s place
6	A number is divisible by 6 if a number is divisible by 2 and 3 both
7	It must be checked by actual division
8	1) For one, two-digit number, three-digit and four-digit number, just check the divisibility by actual division 2) For a number with 4 or more digits is divisible by 8, if the number formed by the last three digits is divisible by 8
9	A number is divisible by 9, if the sum of the digits of a number is divisible by 9
10	A number is divisible by 10 if a number has 0 in the ones
11	A number is divisible by 11 if the difference between the sum of the digits at odd places (from the right) and the sum of the digits at even places (from the right) of the number is either 0 or divisible by 11,

Factorisation and Prime -Factorisation

Factorisation is expressing the number as a product of its factors
So,
36 = 3×12 = 4 X 9
These form is called Factorisation
Prime Factorisation is expressing the number as a product of its prime factors
$36 = 2 \times 2 \times 3 \times 3$
We can find prime factorisation by dividing the numbers with 2, 3, 5, 7 etc. in this order repeatedly so long as the quotient is divisible by that number

HCF and LCM

a. The Highest Common Factor (HCF) of two or more given numbers is the highest of their common factors. It is also known as Greatest Common Divisor (GCD).
Steps to find HCF or GCD
a. Find the prime factorisation of the numbers
b. Choose the common factors in them
c. Multiply those common factors to obtain HCF.

Example
(a) Find the HCF of 8 and 12
Prime Factorisation of the numbers
$8 = 2 \times 2 \times 2$
$12 = 2 \times 2 \times 3$
Common factors are 2,2
So $H C F = 2 \times 2 = 4$
(b) Find the HCF of 20, 28 and 36
Prime Factorisation of the numbers
$20 = 2 \times 2 \times 5$
$28 = 2 \times 2 \times 7$
$36 = 2 \times 2 \times 3 \times 3$
Common factors are 2,2
So $H C F = 2 \times 2 = 4$

(b) The Lowest Common Multiple (LCM) of two or more given numbers is the lowest of their common multiples.
Steps to find LCM
(a) Find the prime factorisation of the numbers
(b) look for the maximum occurrence of all the prime factors in these numbers
(c) The LCM of the numbers will be the product of the prime factors counted the maximum number of times they occur in any of the numbers

Example
(a) Find the LCM of 8 and 12
Prime Factorisation of the numbers
$8 = 2 \times 2 \times 2$
$12 = 2 \times 2 \times 3$
So, $L C M = (2 \times 2 \times 2) \times (3) = 24$

LCM using division method
Here we divide the given numbers by common prime number until the remainder is a prime number or one. LCM will be the product obtained by multiplying all divisors and remaining prime numbers.
Steps are
(1) We place number in the line
(2) We start dividing the number by least prime number which is common among all of them or group of them
(3) Keep dividing by least until we have 1's in the remainder
(4) LCM is the product of the divisors

HCF using Long Division Method

L C M = 2 \times 2 \times 3 \times 3 \times 11 = 396

Real life problems related to HCF and LCM

Example: 1

There are two containers having 240 litres and 1024 litres of petrol respectively. Calculate the maximum capacity of a container which can measure the petrol of both the containers when used an exact number of times.

Solution:

As we have to find the capacity of the container which is the exact divisor of the capacities of both the containers, i. e. maximum capacity, so we need to calculate the HCF.

The common factors of 240 and 1024 are 2 × 2 × 2 × 2. Thus, the HCF of 240 and 1024 is 16. Therefore, the maximum capacity of the required container is 16 litres.

Example: 2
What could be the least number which when we divide by 20, 25 and 30 leaves a remainder of 6 in every case?
Solution:
As we have to find the least number so we will calculate the LCM first.

LCM of 20, 25 and 30 is 2 × 2 × 3 × 5 × 5 = 300.

Here 300 is the least number which when divided by 20, 25 and 30 then they will leave remainder 0 in each case. But we have to find the least number which leaves remainder 6 in all cases. Hence, the required number is 6 more than 300.

The required least number = 300 + 6 = 306.

ASSIGNMENTS

Do Chapter-3, Exercises A to J full + Mental Maths, MCQs and Chapter Test in ex-bk.

R/17

24/08/2021, 26/08/2021, 27/08/2021

Chapter-10 Plane Figures

TOPIC

Quadrilaterals

Types of Quadrilaterals and their properties

Circles

Components of Circles

Drawing a circle

EXPLAINED

Quadrilaterals

Types of Quadrilaterals and their properties

Circles

Components of Circles

Drawing a circle

MUST WATCH FOR BETTER UNDERSTANDING

Video-1 Quadrilateral

Video-2 Types of Quadrilaterals-I

Video-3 Types of Quadrilaterals-II

Video-4 Types of Polygon

Video-5 Drawing Circle

Main Teachings

Oral Explanation Online with some written work.

What is Quadrilateral?

In geometry, a quadrilateral can be defined as a closed, two-dimensional shape which has four straight sides. The polygon has four vertices or corners.

We can find the shape of quadrilaterals in various things around us, like in a chess board, a deck of cards, a kite, a tub of popcorn, a sign board and in an arrow.

Quadrilateral real-life examples we see around us

Properties of a Quadrilateral:

A quadrilateral has 4 sides, 4 angles and 4 vertices.
A quadrilateral can be regular or irregular.
The sum of all the interior angles of a quadrilateral is 360°.

Types of Quadrilaterals

Quadrilaterals can be classified into Parallelograms, Squares, Rectangles and Rhombuses. Square, Rectangle and Rhombus are also Parallelograms.

Here’s a list of the types of quadrilaterals with their name, pictures and properties:

Name of the Quadrilateral:	Picture of Quadrilateral:	Properties of the Quadrilateral:
Parallelogram		Opposite sides are parallel. Opposites sides are equal. Opposite angles are equal.
Square		All sides are equal. All angles are equal and measure 90°.
Rectangle		Opposite sides are parallel. Opposites sides are equal. All angles are equal and measure 90°.
Rhombus		All sides are equal. Opposite angles are equal.
Trapezoid		Opposite sides are parallel. Adjacent angles add up to 180°.

Fun Facts

The word quadrilateral has originated from two Latin words quadri which means “four” and, latus meaning “side”.

What is a Circle?

A circle is a two-dimensional figure formed by a set of points that are at a constant or at a fixed distance (radius) from a fixed point (center) in the plane. The fixed point is called the origin or center of the circle and the fixed distance of the points from the origin is called the radius

Parts of a Circle

A circle has mainly the following parts:

Circumference: Circumference of a circle, also referred to as the perimeter of a circle is the distance around the boundary of the circle.
Radius of Circle: Radius is the distance from the center of a circle to any point on the boundary of the circle. A circle has many radii as it is the distance from the center and touch the boundary of the circle at various points
Diameter: A diameter is a straight line passing through the center that connects two points on the boundary of the circle. We should note that there can be multiple diameters in the circle, but they should:

pass through the center.
be straight lines.
touch the boundary of the circle at two points.

Chord of circle: A chord of a circle is any line segment touching the circle at two different points on its boundary.
Tangent in Circle: A tangent of a circle is a line that touches the circle at a unique point.
Secant in circle: A line that intersects two points on an arc/circumference of a circle is called the secant.
Arc of a Circle: An arc of a circle is referred to as a curve, that is a part or portion of its circumference.
Segment in a Circle: The area enclosed by the chord and the corresponding arc in a circle is called a segment. There are two types of segments - minor segment, and major segment.
Sector of a Circle: The sector of a circle is defined as the area enclosed by two radii and the corresponding arc in a circle. There are two types of sectors, minor sector, and major sector.

What Are Concentric Circles?

Concentric circles are circles with the same or common center. In other words, if two or more circles have the same center point, they are termed as concentric circles. The following figure shows two concentric circles with the same center O.

Half a circle. A closed shape consisting of half a circle and a diameter of that circle*.

A semicircle is a half circle, formed by cutting a whole circle along a diameter line, as shown above. Any diameter of a circle cuts it into two equal semicircles.

For better understanding observe the given image depicting all the parts of a circle.

Circle Formulas

Let's see the list of important formulae pertaining to any circle.

Area of a Circle Formula: The area of a circle refers to the amount of space covered by the circle. The area of a circle totally depends on the length of its radius. Area = π×r²
Circumference of a Circle Formula: The circumference of a circle is the whole length of the circle(boundary). Circumference of circle = 2 × π × r.

Construction of a Circle of a given radius

A circle is a combination of points such that every point is equidistant from the centre.

Example: Draw a circle of radius 3.2 cms.

Open the compasses and measure a distance of 3.2 cm on the ruler. To do this one, metal end tip of the compass should be placed at zero and the pencil should be at 3.2 cms.

Mark a point with a sharp pencil where we want the centre of the circle to be. Name it as O.
Place the pointer ( metal tip) of the compasses on O. The width of the compass should not be altered.
Turn the compasses slowly to draw the circle. Please see that the movement is completed around in one instant.

What is a polygon?

In geometry, a polygon can be defined as a flat or plane, two-dimensional closed shape with straight sides. It does not have curved sides.

Here are a few examples of polygons.

Polygons can be of two types:

Regular Polygons – Polygons that have equal sides and angles are regular polygons.

Here are a few examples of regular polygons.

Irregular Polygons – Polygons with unequal sides and angles are irregular polygons.

Here are a few examples of irregular polygons.

Types of Polygons

ASSIGNMENTS

Do Chapter-10 Exercises- C,D,E + Mental Maths and Chapter Test.

R/16

10/08/2021

Chapter- 10 Plane Figures

( Download Ch-10 in pdf by clicking on the chapter's name above.)

TOPIC

~Open and closed figures

~Interior and exterior of closed figures

~Curvilinear and linear boundaries

~Describing vertices, sides, angles, interior and exterior, altitude and median of a triangle

~Classifying triangles into different types on the basis of their angles and sides

EXPLAINED

~Open and closed figures

~Interior and exterior of closed figures

~Curvilinear and linear boundaries

~Describing vertices, sides, angles, interior and exterior, altitude and median of a triangle

~Classifying triangles into different types on the basis of their angles and sides

MUST WATCH FOR BETTER UNDERSTANDING

Video-1 Plane Figures in Geometry

Video-2 Interior and exterior of closed figures

Video-3 Linear and curvilinear boundaries

Video-4 Introduction to Triangles

Video-5 Altitude and Median of Triangle

Video-6 Different types of Triangles

Main Teachings

Oral Explanation Online with some written work.

ASSIGNMENTS

Study and practice pages 184-188 and do Chapter-10 Exercises A+B.

R/15

27/07/2021, 29/07/2021, 30/07/2021, 03/08/2021, 05/08/2021, 06/08/2021

Ch- 8 Ratio, Proportion and Unitary Method

(Download Ch- 8 in pdf by clicking on the chapter's name above.)

TOPIC

Ratio as one of the different ways of comparing two quantities

Different ways of comparison of quantities through operation of subtraction and through ratio

The concept of Proportion

Understand how ratio and proportion are related to Unitary Method

EXPLAINED

Ratio as one of the different ways of comparing two quantities

Different ways of comparison of quantities through operation of subtraction and through ratio

The concept of Proportion

Understand how ratio and proportion are related to Unitary Method

MUST WATCH FOR BETTER UNDERSTANDING

Video-1 Introduction to Ratio

Video-2 Proportion

Video-3 Unitary Method

Main Teachings

Oral Explanation Online with some written work.

Ratio

If we compare two quantities using division then it is called ratio. It compares quantities in terms of ‘How many times’. The symbol to represent ratio is “:”.

It reads as “4 is to 3”

It can also be written as 4/3.

Example

If there are 35 boys and 25 girls in a class, then what is the ratio of

Number of boys to total students
Number of girls to total students.

Solution

In the ratio, we want the total number of students.

Total number of students = Number of boys + Number of girls

35 + 25 = 60

Ratio of number of boys to total number of students

The ratio of the number of girls to the total number of students

The unit must be same to compare two quantities

If we have to compare two quantities with different units then we need to convert them in the same unit .then only they can be compared using ratio.

Example

What is the ratio of the height of Raman and Radha if the height of Raman is 175 cm and Radha is 1.35 m?

Solution

The unit of the height of Raman and Radha is not same so convert them in the same unit.

Height of Radha is 1.35 m = 1.35 × 100 cm = 135 cm

The ratio of the height of Raman and Radha

The Lowest form of the Ratio

If there is no common factor of numerator and denominator except one then it is the lowest form of the ratio.

Example

Find the lowest form of the ratio 25: 100.

Solution

The common factor of 25 and 100 is 25, so divide both the numerator and denominator with 25.

Hence the lowest ratio of 25: 100 is 1: 4.

Proportion

If we say that two ratios are equal then it is called Proportion.

We write it as a: b : : c: d or a: b = c: d

And reads as “a is to b as c is to d”.

Example

If a man runs at a speed of 20 km in 2 hours then with the same speed would he be able to cross 40 km in 4 hours?

Solution

Here the ratio of the distances given is 20/40 = 1/2 = 1: 2

And the ratio of the time taken by them is also 2/4 = 1/2 = 1: 2

Hence the four numbers are in proportion.

We can write them in proportion as 20: 40 : : 2: 4

And reads as “20 is to 40 as 2 is to 4”.

Extreme Terms and Middle Terms of Proportion

The first and the fourth term in the proportion are called extreme terms and the second and third terms are called the Middle or the Mean Terms.

In this statement of proportion, the four terms which we have written in order are called the Respective Terms.

If the two ratios are not equal then these are not in proportion.

Example 1

Check whether the terms 30,99,20,66 are in proportion or not.

Solution 1.1

To check the numbers are in proportion or not we have to equate the ratios.

As both the ratios are equal so the four terms are in proportion.

30: 99 :: 20: 66

Unitary Method

If we find the value of one unit then calculate the value of the required number of units then this method is called the Unitary method.

Example 1

If the cost of 3 books is 320 Rs. then what will be the cost of 6 books?

Solution 1

Cost of 3 books = Rs. 320

Cost of 1 book = 320/3 Rs.

Cost of 6 books = (320/3) × 6 = 640 Rs.

Hence, the cost of 6 books is Rs. 640.

ASSIGNMENTS

Do Chapter-8 Exercises A,B,C,D,E,F, + Mental Maths, Multiple Choice Questions and Chapter Test pages 162-164.

R/14

13/07/2021, 15/07/2021, 16/07/2021, 20/07/2021, 22/07/2021, 23/07/2021

Chapter- 2 Whole Numbers

( Download Ch- 2 in pdf by clicking on the chapter's name above. )

TOPICS
~1. Introduction to Whole Numbers and Natural Numbers

~2. Performing Operations on Whole numbers like Addition, Subtraction, Multiplication and Division
~3. Understanding Order of Operations
~4. Explore the Number Patterns

EXPLAINED
Introduction to Whole Numbers and Natural Numbers
Performing Operations on Whole numbers like Addition, Subtraction, Multiplication and Division
Understanding Order of Operations
Explore the Number Patterns

MUST WATCH FOR BETTER UNDERSTANDING

Video-1 Introduction ( Whole Numbers )

Video-2 Properties of Whole Numbers

Video-3 Order of Operations

Video-4 Number Patterns

Main Teachings

Oral Explanation Online with some written work.

Properties of Addition
Closure property:

For any two whole numbers a and b, their sum a + b is always a whole number.
E.g. 12 + 45 = 57

12, 45 and 57 all are whole numbers.

Commutative property:

For any two whole numbers a and b, a +b = b + a We can add any two whole numbers in any order.
E.g 12 + 45 = 45 + 12

Associative property
For any three whole numbers a, b and c, (a + b) + c = a + (b + c). , This means the sum is regardless of how grouping is done.
E.g 31 + (24 + 38) = (31 + 24) + 38

Additive identity property:
For every whole number a, a + 0 = a. Therefore ‘0’ is called the Additive identity.
E.g. 19 + 0 = 19

Properties of Subtraction
Closure property:

For any two whole numbers, a and b, if a > b then a – b is a whole number and if a < b then a – b is never a whole number. Closure property is not always applicable to subtraction.
E.g. 150 – 100 = 50, is a whole number but 100 – 150 = -50 is not a whole number.

Commutative property: For any two whole numbers a and b, a – b ≠ b – a . Hence subtraction of whole number is not commutative.
E.g 16 – 7 = 9 but 7 – 16 ≠ 9

Associative property:
For any three whole numbers a, b and c, (a – b) – c ≠ a – (b – c). Hence subtraction of whole numbers is not associative.
E.g. 25 – (10 – 4) = 25 – 6 = 19
(25 – 10) – 4 = 15 – 4 = 11
This means that 25 – (10 – 4) ≠ (25 – 10) – 4

Properties of Multiplication:

Closure property:
For any two whole numbers a and b,their product ax b is always a whole number.
E.g. 12 x 7 = 84, 12, 7 and 84 all are whole numbers.

Commutative property:
For any two whole numbers a and b, a a x b = b x a Order of multiplication is not important.
E.g 11 x 6 = 66 and 6 x 11 = 66
Therefore, 11 x 6 = 6 x 11

Associative property:
For any three whole numbers a, b and c, (a x b) x c = a x (b x c), this means the product is regardless of how grouping is done.
E.g 8 x (4 x 5) = 8 x 20 = 160; (8 x 4) x 5 = 32 x 5 = 160
Therefore, 8 x (4 x 5) = (8 x 4) x 5

Multiplicative identity:
For any whole number a, a x 1 = a Since any number multiplied by 1 doesn’t change its identity hence 1 is called as multiplicative identity of a whole number. E.g. 21 x 1 = 21

Multiplication by zero:
For any whole number a, a x 0 = 0,
E.g 25 x 0 = 0

Distributive property of multiplication over Addition:
This property is used when we have to multiply a number by the sum.
For any three whole numbers a, band c a × (b + c) = a × b + a × c
In order to verify this property, we take any three whole numbers a, b and c and find the values of the expressions a × (b + c) and a × b + a × c as shown below:
Find 3 × (4 + 5).
In this case either you can add the numbers 4 and 5 and then multiply them by 3
3 × (4 + 5) = 3 × 9 = 27
OR you can multiply each addend by 3 and then add the products
3 × 4 + 3 × 5 = 12 + 15 = 27
Therefore, 3 × (4 + 5) = 3 × 4 + 3 × 5

Properties of Division

Closure property:
For any two whole numbers a and b, a ÷ b is not always a whole number. Hence closure property is not applicable to division.
E.g. 68 and 5 are whole numbers but 68 ÷ 5 is not a whole number.

Commutative property:
For any two whole numbers a and b, a ÷ b ≠ b ÷ a. This means division of whole number is not commutative.
E.g. 16 ÷ 4 ≠ 4 ÷ 16

Associative property:
For any 3 whole numbers a, b and c,(a ÷ b) ÷ c ≠ a ÷ (b ÷ c)

E.g. consider (80 ÷ 10) ÷ 2 = 8 ÷ 2 = 4
80 ÷ (10 ÷2) = 80 ÷ 5 = 16
(80 ÷ 10) ÷ 2 ≠80 ÷ (10 ÷2)
Hence division does not follow associative property.

Division by 1
For any whole number a, a ÷ 1 = a, this means any whole number divided by 1 gives the quotient as the number itself.
E.g. 14 ÷ 1 = 14; 26 ÷ 1 = 26

Division of 0 by any whole number
For any whole number, a ≠ 0, 0 ÷ a = 0, this shows zero divided by any whole number (other than zero) gives the quotient as zero.
E.g. 0 ÷ 1 = 0; 0 ÷ 25 = 0;

Division by 0
To divide any number, say 7 by 0, we first have to find out a whole number which when multiplied by 0 gives us 7. This is not possible. Therefore, division by 0 is not defined.

Patterns in whole number
A pattern is a sequence of numbers or picture.

Number Patterns
The order of Operations is the rule in math that states we evaluate the parentheses/brackets first, the exponents/the orders second, division or multiplication third (from left to right, whichever comes first), and the addition or subtraction at the last (from left to right, whichever comes first).

ASSIGNMENTS
Do Exercise ( 2A, 2B, 2C, 2D, 2E ) , Mental Maths, Multiple Choice Questions and Chapter Test page nos 51-52.

R/13

01/07/2021, 02/07/2021, 06/07/2021, 08/07/2021, 09/07/2021

Chapter- 9 Basic Geometric Figures

TOPICS

Measuring Line Segments

Angles and it's elements

Measuring and drawing angles using a protractor

Classify angles into different types

EXPLAINED

Measuring Line Segments

Angles and it's elements

Measuring and drawing angles using a protractor

Classify angles into different types

MUST WATCH FOR BETTER UNDERSTANDING

Video-1 Measuring Line Segments

Video-2 Angles

Video-3 Measuring and drawing angles

Video-4 Types of Angles

Main Teachings

Oral Explanation Online with some written work.

ASSIGNMENTS

Do Exercise (9B, 9C, 9D) and Mental Maths, Multiple Choice Questions + Chapter Test page nos 181-183.

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

R/12

15/06/2021, 17/06/2021, 18/06/2021
REVISION
Chapter- 7 Algebra

Chapter- 9 Basic Geometric Figures

(Download Ch- 9 in pdf by clicking on the chapter's name above.)

TOPICS

Points, Lines and Planes

Rays and Line Segments

Classifying Lines and Pairs of Lines

EXPLAINED

Points, Lines and Planes

Rays and Line Segments

Classifying Lines and Pairs of Lines

MUST WATCH FOR BETTER UNDERSTANDING

Video-1 Basic Geometric Figures

Main Teachings

Oral Explanation Online with some written work.

ASSIGNMENTS

Revise Ch-7 all exs + Study and practice Ch-9 page nos 167-171 and do Exercise-9A full.

R/11

08/06/2021, 10/06/2021, 11/06/2021
Chapter- 7 Algebra

TOPIC
Solving Equations by Transposition Method
Word Problems into Equations
Solving Two Steps Equations
Algebra as Generalisation

EXPLAINED
Solving Equations by Transposition Method
Word Problems into Equations
Solving Two Steps Equations
Algebra as Generalisation
MUST WATCH FOR BETTER UNDERSTANDING
Video-1 Solving Equations by Transposition Method
Video-2 Word Problems into Equations
Video-3 Solving Two Steps Equations
Video-4 Algebra as Generalisation
Main Teachings
Oral Explanation Online with some written work.
ASSIGNMENTS:
Do Exercise ( 7E, 7F, 7G, 7H ) and also do Mental Maths, Multiple Choice Questions + Chapter Test page nos. 146-147.

R/10

04 / 06 / 2021

Chapter- 7 Algebra

TOPIC

Equations

Solving Equations by Inspection

Solving Equations by Using Inverse Operations

EXPLAINED

Equations

Solving Equations by Inspection

Solving Equations by Using Inverse Operations

MUST WATCH FOR BETTER UNDERSTANDING

Video-1 Equation

Video-2 Solving Equations by Inspection

Video-3 Solving Equations by Using Inverse Operations

Main Teachings

Oral Explanation Online with some written work.
ASSIGNMENTS
Do Exercise (7C and 7D) full.

R/9

03 / 06 / 2021

Chapter- 7 Algebra
(Download Ch-7 in pdf by clicking on the chapter's name above.)

TOPIC
Introduction
Using Mathematical Operating Symbols in Algebra
Translating Words into Algebraic Symbols
Evaluating Algebraic Expressions

EXPLAINED
Introduction
Using Mathematical Operating Symbols in Algebra
Translating Words into Algebraic Symbols
Evaluating Algebraic Expressions
MUST WATCH FOR BETTER UNDERSTANDING
Video-1 Introduction
Video-2 What is Algebra?
Video-3 Variables and Constant
Video-4 Rules Using Algebra
Video-5 Evaluating Algebraic Expressions
Main Teachings
Oral Explanation Online with some written work.
ASSIGNMENTS
Do Exercise (7A and 7B) full.

R/8

01 / 06 / 2021

REVISION

Chapter-1

ASSIGNMENTS

Revise Ch-1 all exercises.

R/7

28 / 05 / 2021

Chapter- 1 Knowing Our Numbers

TOPIC

Use of Brackets

EXPLAINED

Use of Brackets

MUST WATCH FOR BETTER UNDERSTANDING

Video-1 Use of Brackets

Main Teachings

Oral Explanation Online with some written work.

USE OF BRACKETS
Brackets help in simplifying an expression that has more than one mathematical operation.
If an expression that includes the brackets is given, then perform the operation inside the bracket and change every thing into a single number. Then carry out the operation that lies outside the bracket.
e.g.
1. (6 + 8) x 10 = 14 x 10 = 140

2. (8 + 3) (9 - 4) = 11 x 5 = 55

ASSIGNMENTS

Do Exercise 1 M full + Mental Maths and Chapter Test pages 34-36.

R/6

25 / 05 / 2021

Chapter- 1 Knowing Our Numbers

TOPIC

The International System of Numeration

Roman Numerals

EXPLAINED

The International System of Numeration

Roman Numerals

MUST WATCH FOR BETTER UNDERSTANDING

Video-1 The International System of Numeration

Video-2 Roman Numerals

Main Teachings

Oral Explanation Online with some written work.

International system of numeration
Values of the places in the International system of numeration are Ones, Tens, Hundreds, Thousands, Ten thousands, Hundred thousands, Millions, Ten millions and so on.
1 million = 1000 thousands,
1 billion = 1000 millions

Following place value chart can be used to identify the digit in any place in the International system.

Periods

Billions

Millions

Thousands

Ones

Places

Hundreds

Tens

Ones

Hundreds

Tens

Ones

Hundreds

Tens

Ones

Hundreds

Tens

Ones

(ii) 56,789,056Commas in International system of Numeration

As per International numeration system, the first comma is placed after the hundreds place. Commas are then placed after every three digits.

e.g. (i) 8,876,547
The number can be read as eight million eight hundred seventy-six thousand five hundred and forty-seven.

The number can be read as fifty-six million seven hundred eighty-nine thousand and fifty-six.

Roman Numerals
The number system invented by Romans is called Roman number system or Roman Numerals.

Symbol	Value	Repitition Allowed
I	1	Yes (3 times at max)
V	5	No
X	10	Yes (3 times at max)
L	50	No
C	100	Yes (3 times at max)
D	500	No
M	1000	Yes (3 times at max)

If a symbol is repeated, its value is added as many times as it occurs. Examples,Rules for writing Roman Numerals:

1. II = 2
2. CCC = 300
A symbol is not repeated more than three times. But the symbols V, L and D are never repeated. Example,
1. XX is correct but DD is not.
If a symbol of smaller value is written to the right of a symbol of greater value, its value gets added to the value of greater symbol. Example,
1. XI = 11
2. VII = 7
If a symbol of smaller value is written to the left of a symbol of greater value, its value is subtracted from the value of the greater symbol. Example,
1. IX = 9
2. XC = 90
The symbols V, L and D are never written to the left of a symbol of greater value, i.e. V, L and D are never subtracted. The symbol I can be subtracted from V and X only. The symbol X can be subtracted from L, M and C only.

Problem: Write in Roman Numerals.

Solution:

(a) 73

73 = 70 + 3

70 = 50 + 10 + 10 = LXX

3 = 1 + 1 + 1 = III

Hence 73 can be written as LXXIII

(b) 92

92 = 90 + 2

90 = 100 - 10 = XC

2 = 1 + 1 = II

Hence 92 can be written as XCII

ASSIGNMENTS

Do Exercises 1K and 1L full.

R/5

21 / 05 / 2021

Chapter-1 Knowing Our Numbers

TOPIC

Comparing and Ordering Large Numbers

Use of Numbers in Every day Life

EXPLAINED

Comparing and Ordering Large Numbers

Use of Numbers in Every day Life

MUST WATCH FOR BETTER UNDERSTANDING

Video-1 Use of Numbers in Every day Life

Main Teachings

Oral Explanation Online with some written work.

Comparison of Numbers
We often need to compare the two or more numbers. Here are some of the ways it can be performed easily
1) If two numbers have unequal number of digits, then the number with the greater number of digits is greater.
2) If two numbers have equal number of digits then, the number with greater valued digit on the extreme left is greater. If the digits on extreme left of the numbers are equal then the digits to the right of the extreme left digits are compared and so on.
Example
a) Comparison between 358 and 4567
Answer
Here 4567 has four digits and 358 has three digits, so clearly 4657 is greater than 358

b) Comparison between 1345 and 2456
Answer
Here both the number have same digit, So we need start looking at the extreme left digit
1345 -> 1
2456 -> 2
Now 2 > 1
So we can clearly state 2456 > 1345
Use of Numbers in Every day Life

ASSIGNMENTS
Do Exercises 1I and 1J full.

R/4

18 / 05 / 2021

Chapter-1 Knowing Our Numbers

TOPIC
Extension To Large Numbers
Extending the concepts of Place value, Expanded Form and Comparison of Numbers to Large Numbers

EXPLAINED
Extension To Large Numbers
Extending the concepts of Place value, Expanded Form and Comparison of Numbers to Large Numbers

MUST WATCH FOR BETTER UNDERSTANDING
Video-1 Introducing Large Numbers

Video-2 Indian System of Numeration

Video-3 Place value , Face Value and Expanded Form

Main Teachings

Oral Explanation Online with some written work.

Introducing Large Numbers
What is the Indian Numeral System?
The Indian numeral system contains numerals that are used to represent the numbers using a set of symbols. This system can be distinguished from the other numeral systems based on the nomenclature followed for different place values. When we use the Indian numeral system, we count with ones, tens, hundreds, thousands, ten thousands, lakhs, ten lakhs, and crores.

The following table depicts the different periods and places according to the number of digits in a number.
Use of Commas
According to the Indian numeral system, separators (comma) are used after every period while representing a number in its standard numeral form. For example, the number 384756182 can be better represented as 38,47,56,182 in the standard Indian numeral system form using separators after every period.

The number name for 38,47,56,182 is written as thirty-eight crore, forty-seven lakh fifty-six thousand, one hundred and eighty-two.

Place value and face value:
The place value of a digit of a number depends upon its position in the number. The face value of a digit of a number does not depend upon its position in the number. It always remains the same wherever it lies regardless of the place it occupies in the number.

Example: Let us see the place value and face value of the underlined digit in the number 1,32,460. The digit 2 in the number 1,32,460 lies in the thousands period (1000) and hence the place value of 2 is 2 thousands (or 2000). The face value of 2 is 2 only.

Expanded form:
When a number is written as the sum of the place values of all the digits of the number, then the number is in its expanded form.

Example: The expanded form of 9,67,480 is as shown below:
9,67,480 = 900000 + 60000 + 7000+400+80.

ASSIGNMENTS
Do Exercises-1G and 1H full.

R/3

11 / 05 / 2021

Chapter-1 Knowing Our Numbers

TOPIC

Estimation and Rounding Off

Estimating Sums, Differences, Products and Quotients

EXPLAINED

Estimation and Rounding Off

Estimating Sums, Differences, Products and Quotients

MUST WATCH FOR BETTER UNDERSTANDING

Video-1 Rounding Off Numbers

Video-2 Estimation

Main Teachings

Oral Explanation Online with some written work.

The estimation of a number is a reasonable guess of the actual value. Estimation means approximating a quantity to the accuracy required. This is done by rounding off the numbers involved and getting a quick and rough answer.

Rounding off a number to the nearest tens

The numbers 1, 2, 3 and 4 are nearer to 0. So, these numbers are rounded off to the lower ten. The numbers 6, 7, 8 and 9 are nearer to 10. So, these numbers are rounded off to the higher ten. The number 5 is equidistant from both 0 and 10, so it is rounded off to the higher ten.

e.g.

(i) We round off 31 to the nearest ten as 30

(ii) We round off 57 to the nearest ten as 60

(iii) We round off 45 to the nearest ten as 50

Rounding off a number to the nearest hundreds

The numbers 201 to 249 are closer to 200. So, these numbers are rounded off to the nearest hundred i.e. 200. The numbers 251 to 299 are closer to 300. So, these numbers are rounded off to the higher hundred i.e. 300. The number 250 is rounded off to the higher hundred.

e.g.

(i) We round off 578 to the nearest 100 as 600.

(ii) We round off 310 to the nearest 100 as 300.

Rounding off a number to the nearest thousands

Similarly, 1001 to 1499 are rounded off to the lower thousand i.e.1000, and 1501 to 1999 to the higher thousand i.e. 2000. The number 1500 is equidistant from both 0 and 1000, and so it is rounded off to the higher thousand i.e.2000.

e.g.

(i) We round off 2574 to the nearest thousand as 3000.

(ii) We round off 7105 to the nearest thousand as 7000.

Estimation of sum or difference:

When we estimate sum or difference, we should have an idea of the place to which the rounding is needed.

e.g.

(i) Estimate 4689 + 19316

We can say that 19316 > 4689

We shall round off the numbers to the nearest thousands.

19316 is rounded off to 19000

4689 is rounded off to 5000

Estimated sum:

19000 + 5000 = 24000

(ii) Estimate 1398 – 526

We shall round off these numbers to the nearest hundreds.

1398 is rounded off to 1400

526 is rounded off to 500

Estimated difference:

1400 – 500 = 900

Estimation of the product:

To estimate the product, round off each factor to its greatest place, then multiply the rounded off factors.

e.g.

Estimate 92 x 578

The first number, 92, can be rounded off to the nearest ten as 90.

The second number, 578, can be rounded off to the nearest hundred as 600.

Hence, the estimated product =90 x 600 = 54,000.

Estimating the outcome of number operations is useful in checking the answer.

Estimating Quotients

It is easier a quotient by using compatible numbers close to the divisor and the dividend, i.e., choosing a pair of numbers that are easier to divide mentally.

ASSIGNMENTS

Do Exercises 1E and 1F full.

R/2

07 / 05 / 2021

Chapter-1 Knowing Our Numbers

TOPIC

Building Numbers

Ascending order and Descending Order

EXPLAINED

Building Numbers

Ascending order and Descending Order

MUST WATCH FOR BETTER UNDERSTANDING

Video-1 Forming Numbers

Main Teachings

Oral Explanation Online with some written work.
Arranging numbers in ascending order and descending order.
We know, while arranging numbers from the smallest number to the largest number, then the numbers are arranged in ascending order.
Suppose for example, 81, 97, 123, 137 and 201 are arranged in ascending order.

Vice-versa while arranging numbers from the largest number to the smallest number then the numbers are arranged in descending order.
Suppose for example, 187, 121, 117, 103 and 99 are arranged in descending order.

Building Numbers

In formation of numbers with the given digits we may say that a number is an arranged group of digits. Numbers may be formed with or without the repetition of digits. Let us observe some of the formation of numbers without the repetition of digits.

Some numbers formed by 3 digits are given below:

(a) The numbers by 2, 3, and 4 are:

234, 243, 324, 342, 423, 432 (6 numbers each of 3 digits)

How many numbers in all can we have with 4 digits ?

The smallest 4-digit number = 1000.

The greatest 4-digit number = 9999.

There for 9999 - 1000 = 8999 and 8999 + 1 = 9000

So, we say that we have 9000 four-digit numbers.

ASSIGNMENTS
Do Exercises 1C and 1D full.

R/1

04 / 05 / 2021

Ch-1 Knowing Our Numbers

(Download Ch-1 in pdf by clicking on the chapter name above.)

TOPIC
Introduction
Natural Numbers
Hindu Arabic Number System
Comparing Numbers
Successor and Predecessor

EXPLAINED
Natural number and it's symbols.
Hindu- Arabic Number System
Comparing numbers, Successor and Predecessor

MUST WATCH FOR BETTER UNDERSTANDING
Video-1 Introduction
Video-2 Natural and Whole Numbers
Video-3 Compare Numbers
Main Teachings
Oral Explanation Online with some written work.

What are Natural numbers?

Counting numbers 1, 2, 3, 4, ...... etc. are called Natural numbers. The smallest natural number is 1 and there is no largest natural number.

Digits and Place value

Numbers are formed using the ten symbols 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. These symbols are called digits or figures.

To find the place value of a digit in a number, multiply the digit with the value of the place it occupies.

Comparison of Numbers

We often need to compare the two or more numbers. Here are some of the ways it can be performed easily

1) If two numbers have unequal number of digits, then the number with the greater number of digits is greater.

2) If two numbers have equal number of digits then, the number with greater valued digit on the extreme left is greater. If the digits on extreme left of the numbers are equal then the digits to the right of the extreme left digits are compared and so on.

Example

a) Comparison between 358 and 4567

Answer

Here 4567 has four digits and 358 has three digits, so clearly 4657 is greater than 358

Predecessor and Successor

Predecessor

The number which comes before the given number is known as predecessor.

Since 0 is the first whole number it does not have predecessor which is a whole number.

Number Predecessor

20 19

1000 999

1599 1598

Successor

The number which comes after the given number is knows as successor.

Number Successor

0 1

99 100

1999 2000

ASSIGNMENTS

Do Exercise 1(A), and 1B full.

Given Number	Appropriate to Nearest	Rounded Form
75847	Tens	75850
75847	Hundreds	75800
75847	Thousands	76000
75847	Tenth thousands	80000

Tuesday, June 22, 2021

6 MATHEMATICS 2021-2022

Line Segment

Write the numbers in a line so that the decimal points of both the numbers lined up.Then subtract and borrow as we do in whole numbers.Line up the decimal point in the answer also.

The unit must be same to compare two quantities

The Lowest form of the Ratio

Proportion

Extreme Terms and Middle Terms of Proportion

Unitary Method

Introduction

Introduction to numbers

Comparing numbers

Ascending and Descending Order and Shifting Digits

Ascending order and Descending order

How many numbers can be formed using a certain number of digits?

Shifting digits

Place value

Larger Numbers and Estimates

Introducing large numbers

Estimation

Estimating sum or difference

Estimating products of numbers

BODMAS

Using brackets

Introducing Large NumbersWhat is the Indian Numeral System?

Introducing Large Numbers

Place value and face value:

Expanded form:

When a number is written as the sum of the place values of all the digits of the number, then the number is in its expanded form.Example: The expanded form of 9,67,480 is as shown below:9,67,480 = 900000 + 60000 + 7000+400+80.

Roman Numerals

More Examples of Variables

MUST WATCH FOR BETTER UNDERSTANDINGVideo-1 Factors and MultiplesVideo-2 Types of NumbersVideo-3 Divisibility RulesVideo-4 Prime FactorisationVideo-5 HCF and LCMVideo-6 Relationship between HCF and LCMVideo-7 Word Problems on HCF and LCMMain Teachings Oral Explanation Online with some written work.

Ratio

The unit must be same to compare two quantities

The Lowest form of the Ratio

Proportion

Extreme Terms and Middle Terms of Proportion

Unitary Method

CLASS 6 SUBJECT SELECTION

Write the numbers in a line so that the decimal points of both the numbers lined up.
Then subtract and borrow as we do in whole numbers.
Line up the decimal point in the answer also.

Introducing Large Numbers

What is the Indian Numeral System?

When a number is written as the sum of the place values of all the digits of the number, then the number is in its expanded form.
Example: The expanded form of 9,67,480 is as shown below:
9,67,480 = 900000 + 60000 + 7000+400+80.